Question

If from any point $P,$ tangents $PT,P{T}'$ are drawn to two given circles with centers $A$ and $B$ respectively; and if $PN$ is the perpendicular from $P$ on their radical axis, then $P{{T}^{2}}-P{{{T}'}^{2}}=$
$\left( a \right) 2.PN.AB$
$\left( b \right) 4.PN.AB$
$\left( c \right) PN.AB$
$\left( d \right)$ None of these

Answer 1

Hint: We will write the equations of the given two circles. Then we will find the line joining the centers of the two circles. Then, we will find the equation of the tangents. Then, we will find the equation of the radical axis. With this information, we can find the difference of the squares of the tangents.

Complete step-by-step answer:
Let us draw the diagram as follows:

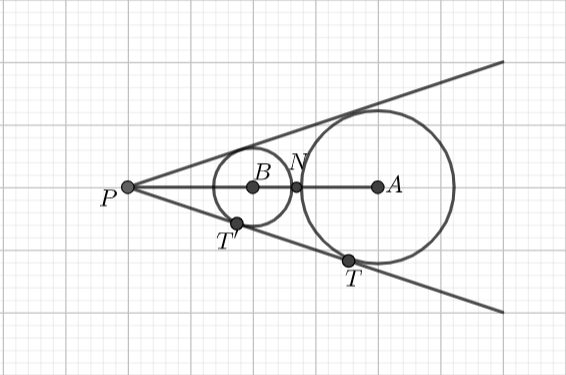
We need to write the equations of the two circles.
Let the equation of the first circle be ${{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+c=0.......\left( 1 \right)$
And let the equation of the second circle be ${{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+c=0.......\left( 2 \right)$
Then, we can say that the centers of the first and second circles are given by $A\left( -{{g}_{1}},0 \right)$ and $B\left( -{{g}_{2}},0 \right)$ respectively.
So, we will get $AB={{g}_{1}}-{{g}_{2}}.$
Now, let us suppose that the point $P$ is given by the coordinates $\left( {{x}_{1}},{{y}_{1}} \right).$
Then, we know that the tangent $PT$ is given by $PT=\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{1}}{{x}_{1}}+c}.$
Similarly, we can write the tangent $P{T}'$ as $P{T}'=\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{2}}{{x}_{1}}+c}.$
Now, we can find the radical axis of the given two circles by finding the difference of the equation $\left( 1 \right)$ and equation $\left( 2 \right).$
Therefore, the radical axis of the circles is given by $2\left( {{g}_{1}}-{{g}_{2}} \right)x=0$ or $x=0.$
We know that $PN$ is the length of the perpendicular from $P$ on the radical axis ${{x}_{1}}.$
Now, we will get $P{{T}^{2}}-P{{{T}'}^{2}}={{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{1}}{{x}_{1}}+c-\left( {{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{2}}{{x}_{1}}+c \right).$
We can write it as $P{{T}^{2}}-P{{{T}'}^{2}}={{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{1}}{{x}_{1}}+c-{{x}_{1}}^{2}-{{y}_{1}}^{2}-2{{g}_{2}}{{x}_{1}}-c.$
After cancelling the similar terms with opposite signs, we will get $P{{T}^{2}}-P{{{T}'}^{2}}=2{{g}_{1}}{{x}_{1}}-2{{g}_{2}}{{x}_{1}}.$
From this, we will get $P{{T}^{2}}-P{{{T}'}^{2}}=2{{x}_{1}}\left( {{g}_{1}}-{{g}_{2}} \right).$
So, we get \[P{{T}^{2}}-P{{{T}'}^{2}}=2.PN.AB.\] \[\]
Hence the answer is $2.PN.AB.$

Note: We know that the standard equation of a circle of radius $r$ and centered at a point $\left( h,k \right)$ is given by ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}.$ The general equation of any type of circle is given by ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0,$ for all values of $g,f$ and $c.$ If we add ${{g}^{2}}+{{f}^{2}}$ on both sides of the general equation and transposing $c$ from the LHS to the RHS will give the standard equation of a circle centered at $\left( g,f \right)$ with a radius of $a$ where ${{g}^{2}}+{{f}^{2}}-c={{a}^{2}}.$