Question

If four squares are chosen at random in a chessboard, the probability that they lie on a diagonal line is \[=\dfrac{91k}{^{64}{{C}_{4}}}\]. Find the value of k.

Answer 1

Hint: Find the total number of ways of selecting 4 squares such that they lie on a diagonal line. Use the idea that for four squares to be on a diagonal line, the diagonal line must be at least four squares long. Use the fact that the longest diagonal line in a chessboard is eight squares long. Find the number of 4 squares long diagonal lines, the number of 5 squares long diagonal lines, the number of 6 squares long diagonal lines, the number of 7 squares long diagonal lines and the number of 8 squares long diagonal lines. Find, in each case, the number of ways of selecting four squares. Hence find the total number of ways in which we can select four squares on a chessboard so that they are on a diagonal line.
Also, find the number of ways of selecting four squares out of given 64 squares. Hence find the probability of the event. Compare with the given probability to get the value of k.

Complete step-by-step answer:
Finding the number of 4 squares long diagonal lines:

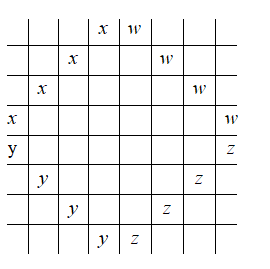
The diagonal lines of length four squares are shown above. As is evident from the above diagram, there are four such lines
Finding the number of 5 squares long diagonal lines:

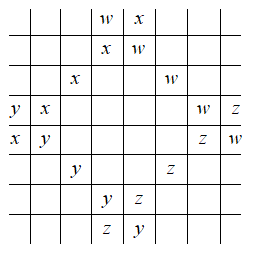
The diagonal lines of length five squares are shown above. As is evident from the above diagram, there are four such lines.
Finding the number of 6 squares long diagonal lines:

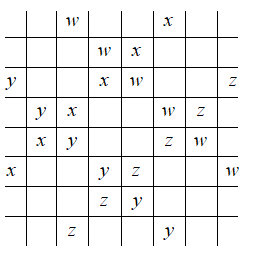
The diagonal lines of length six squares are shown above. As is evident from the above diagram, there are four such lines.
Finding the number of 7 squares long diagonal lines:

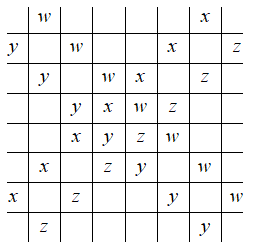
The diagonal lines of length seven squares are shown above. As is evident from the above diagram, there are four such lines.
Finding the number of 8 squares long diagonal lines:

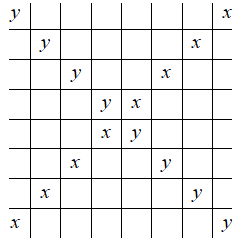
The diagonal lines of length eight squares are shown above. As is evident from the above diagram, there are two such lines.
Now we have the following cases:
Case I: When the chosen four squares lie on a diagonal line of length four squares:
We have 4 choices among the selection of lines and among 4 squares we have to select all the four squares. This can be done in $4{{\times }^{4}}{{C}_{4}}=4$ ways.
Case II: When the chosen four squares lie on a diagonal line of length five squares:
We have 4 choices among the selection of the lines and among 5 squares we have to select 4 squares. This can be done in $4{{\times }^{5}}{{C}_{4}}=20$ ways.
Case III: When the chosen four squares lie on a diagonal line of length six squares:
We have 4 choices among the selection of the lines and among 6 squares we have to select 4 squares. This can be done in $4{{\times }^{6}}{{C}_{4}}=60$ ways.
Case IV: When the chosen four squares lie on a diagonal line of length seven squares:
We have 4 choices among the selection of the lines and among 7 squares, we have to select 4 squares. This can be done in $4{{\times }^{7}}{{C}_{4}}=140$ ways.
Case V: When the chosen four squares lie on a diagonal line of length eight squares:
We have 2 choices among the selection of the lines and among 8 squares, we have to select 4 squares. This can be done in $2{{\times }^{8}}{{C}_{4}}=140$ ways.
Hence the total number of ways of selecting 4 squares, such that they lie on a diagonal line is $4+20+60+140+140=364$
Also, the number of ways of selecting 4 squares out of 64 squares is given by $^{64}{{C}_{4}}$.
Hence the probability that the chosen squares lie on a diagonal line is $\dfrac{364}{^{64}{{C}_{4}}}$
But given that the probability is $\dfrac{91k}{^{64}{{C}_{4}}}$
Hence we have
 $\dfrac{91k}{^{64}{{C}_{4}}}=\dfrac{364}{^{64}{{C}_{4}}}$
Hence, we have
$\begin{align}
  & 91k=364 \\
 & \Rightarrow k=4 \\
\end{align}$
Hence the value of k is 4.

Note: [1] Do not multiply the individual number of ways as this will give the incorrect answer. In finding the total number of ways, we added the individual number of ways in each case. This is done according to the fundamental principle of counting. Since the four squares can lie in either of the cases, hence we have to perform one of these five tasks. Hence the individual number of ways in these tasks are added to get the total.
[2] Alternatively, we can simplify the above calculation by making use of pascal's rule.
Total number of ways
 $\begin{align}
  & \text{ }=4\left( ^{4}{{C}_{4}}{{+}^{5}}{{C}_{4}}+\cdots {{+}^{7}}{{C}_{4}} \right)+2\left( ^{8}{{C}_{4}} \right) \\
 & \text{ }=4\left( ^{5}{{C}_{5}}{{+}^{5}}{{C}_{4}}+\cdots {{+}^{7}}{{C}_{4}} \right)+2\left( ^{8}{{C}_{4}} \right) \\
 & \text{ }=4\left( ^{6}{{C}_{5}}{{+}^{6}}{{C}_{4}}{{+}^{7}}{{C}_{4}} \right)+2\left( ^{8}{{C}_{4}} \right) \\
 & \text{ }=4\left( ^{8}{{C}_{5}} \right)+2\left( ^{8}{{C}_{4}} \right)=364 \\
\end{align}$
[3] The formula for $n\times n$ board in which we have to select r squares on a diagonal line, $r$\begin{align}
  & 4\left( ^{r}{{C}_{r}}{{+}^{r+1}}{{C}_{r}}+\cdots {{+}^{n-1}}{{C}_{r}} \right)+2\left( ^{n}{{C}_{r}} \right) \\
 & \text{ }=4\left( ^{n}{{C}_{r+1}} \right)+2\left( ^{n}{{C}_{r}} \right) \\
 & \text{ }=2\left( ^{n}{{C}_{r+1}} \right)+2\left( ^{n+1}{{C}_{r+1}} \right) \\
\end{align}$
Put n = 9 and r = 4, we get
Number of ways $=2{{\times }^{8}}{{C}_{5}}+2{{\times }^{9}}{{C}_{5}}=364$