Question

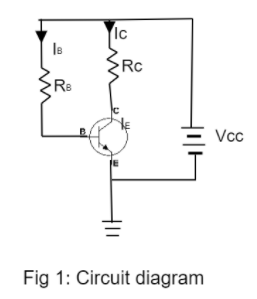
If for the following C-E circuit, $\beta = 100$, ${V_{CE}} = 7V$, \[{V_{BE}}\] is negligible and ${R_C} = 2k\Omega $, then ${i_B}$=?

(a) 0.04 mA
(b) 0.03 mA
(c) 0.02 mA
(d) 0.01 mA

Answer 1

Hint: The configuration in which the emitter is connected between collector and base is called a C-E (common emitter) configuration. In such a circuit, input is provided between emitter and base whereas the output is taken between emitter and collector. Apply Kirchhoff’s law separately in the arms of the circuit to get relation in current and voltage of that arm or node.

Formula Used:
Ohm's law:
$I = \dfrac{V}{R}$
where,
I is current
V is voltage
R is resistance.
Kirchhoff’s Law:
Total current entering the node is the same as total current exiting through any node ( true for randomly chosen any node).
Current gain through the circuit:
$\beta = \dfrac{{{i_C}}}{{{i_B}}}$ …… (1)
Complete step by step answer:
Given:
1. Current gain $\beta = 100$
2. Voltage ${V_{CE}} = 7V$
3. ${R_C} = 2k\Omega $

To find: Find the current ${i_B}$.

Step 1 of 2:
Apply Kirchhoff’s voltage law to the right-hand arm of the circuit. This gives:
$V = {V_{CE}} + {I_C}{R_C}$
$
  15 = 7 + {i_C} \times (2 \times {10^3}) \\
  {i_C} = \dfrac{8}{{2 \times {{10}^3}}} \\
  {i_C} = 4mA \\
 $

Step 2 of 2:
Use eq (1) to find the current gain ${\beta _{AC}}$:
$100 = \dfrac{{4mA}}{{{i_B}}}$ …… (2)
Find ${i_B}$ from eq (2):
$
  {i_B} = \dfrac{{4mA}}{{100}} \\
  {i_B} = 0.04mA \\
 $

Final Answer: In the given circuit, base current ${i_B}$ is (a) 0.04 mA.

Additional Information: In common emitter amplifier circuits, we get large voltage gain and power gain whereas current gain is moderate. This ability of CE transistors is harnessed in developing advanced BJT where we get stable and steady voltage supply, even though there is varying current gain i.e. in the circuit by keeping base biased by DC voltage. Different combinations of these BJT used for making logic gates circuits for computations.

Note: In questions like these, apply Kirchhoff’s voltage law separately for both the arms. Use expression for current gain to find the value of current.