Question

If $f\left( x \right)=a{{x}^{2}}+bx+c$ and a < 0, a point $\alpha $ lie in between the two roots, then $f\left( \alpha \right)$ will always be:
(a) $f\left( \alpha \right)$ will always be positive.
(b) $f\left( \alpha \right)$ will always be negative.
(c) If both roots are negative then $f\left( \alpha \right)$ will be negative.
(d) If one root is negative and one positive then $f\left( \alpha \right)$ will be negative.

Answer 1

Hint: Assume p and q as the two roots of the quadratic equation. Draw the graph of the downward parabola and consider different cases like: both roots negative, both are positive and one negative one positive. Consider the point $\alpha $ on the x – axis and check the corresponding value on the curve of parabola.

Complete step by step answer:
Here we have been provided with the function $f\left( x \right)=a{{x}^{2}}+bx+c$ with the condition a < 0 and it has two roots. We have to determine the sign of $f\left( \alpha \right)$ if $\alpha $ lie in between the two roots.
Clearly we can see that the given function $f\left( x \right)=a{{x}^{2}}+bx+c$ corresponds to a parabola and the condition a < 0 means that it is opening downwards. Let us assume p and q as the roots of this quadratic equation. Let us consider three cases regarding the two roots and examine the situation geometrically.
(1) Here we are considering that both the roots are positive, so we will have the graph as shown below: -

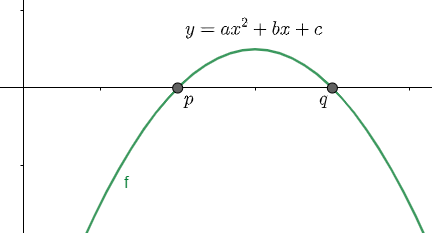
We have assumed a point $\alpha $ between the roots p and q. Clearly we can see that in the range $\left[ p,q \right]$ any value of $\alpha $ will correspond to a point on the parabola above the x – axis, so $f\left( \alpha \right)$ will be positive.
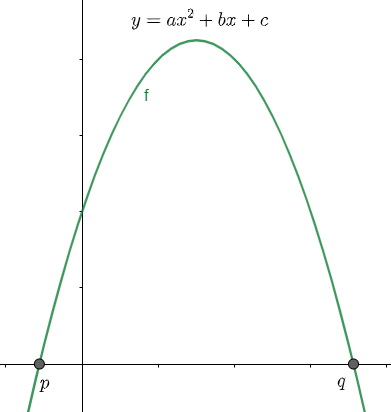
(2) Here we are considering the both the roots are negative, so we will have the graph as shown below:

We have assumed a point $\alpha $ between the roots p and q. clearly we can see that in the range $\left[ p,q \right]$ any value of $\alpha $ will correspond to a point on the parabola above the x – axis, so in this case also $f\left( \alpha \right)$ will be positive.
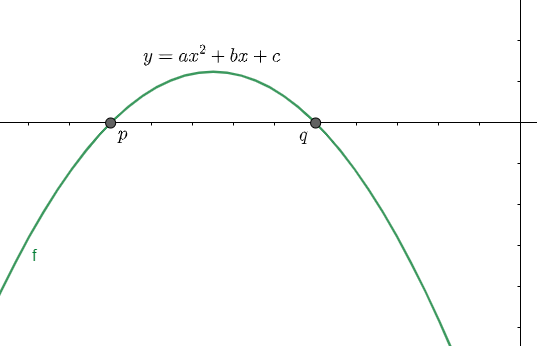
(3) Here we are considering that one root is negative and the other is positive, so we will have the graph as shown below:

We have assumed a point $\alpha $ between the roots p and q. clearly we can see that in the range $\left[ p,q \right]$ any value of $\alpha $ will correspond to a point on the parabola above the x – axis, so in the third case also $f\left( \alpha \right)$ will be positive.
Therefore, $f\left( \alpha \right)$ will always be positive.
So, the correct answer is “Option a”.

Note: Note that if the given condition would have been a > 0 then the parabola would have been opening upward and then the sign of $f\left( \alpha \right)$ for all the values of $\alpha $ in the range $\left[ p,q \right]$. Here we don’t know the values of roots or the quadratic equation, so we cannot judge if both the roots will be positive, negative or one positive and the other negative. This is the reason we have considered all the three cases one by one.