Question

If $f_{0}=5cm$, $\lambda=600A^{\circ}$, $a=1cm$ for a microscope, then what will be its resolving power.
\[\begin{align}
  & A.11.9\times {{10}^{5}}/m \\
 & B.10.9\times {{10}^{5}}/m \\
 & C.10.9\times {{10}^{4}}/m \\
 & D.10.9\times {{10}^{3}}/m \\
\end{align}\]

Answer 1

Hint: From the definition of resolving power and the famous Rayleigh criterion, we can solve the question. The resolving power of a microscope is given by the Abbe’s criterion, using the formula and by plugging in the write values in the respective places; we can find the required answer.

 Formula: $R.P=\dfrac{1}{\Delta d}$

 Complete answer:
Resolving power is the ability of an optical instrument to resolve two points which are close together. Clearly, resolving power depends on the width of the aperture, refractive index of the lens and the wavelength of the incident wavelength. According to Rayleigh criterion, two point sources are said to be just resolved when the principal diffraction maximum of one image coincides with the first minimum of the other. The resolution depends on the ratio of wavelength to the width or how big is the aperture of the optical instrument.
$R.P=\dfrac{1}{\Delta d}$
The resolving power of a microscope is inversely proportional to the distance $\Delta d$ between the two objects which are to be resolved. From Abbe’s criterion, we have $\Delta d = \dfrac{1.22\lambda}{2nsin\theta}$, where $n$ is the refractive index of the lens and $\theta$ is the angle separation, and is as shown below.

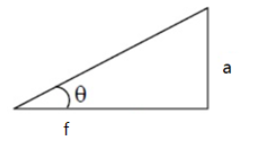
For the given microscope,$f_{0}=5cm$, $\lambda=600A^{\circ}$, $a=1cm$. Let us assume that the refractive index of the lens is $\mu=1$
Clearly, for small angles $tan\theta=sin\theta=\dfrac{a}{f}=\dfrac{1}{5}=0.2$
On substitution,
$\implies R.P=\dfrac{2\times 1\times 0.2}{1.22\times 6\times 10^{-7}}$
$\therefore R.P=10.9\times 10^{5}m^{-1}$ is the required answer.

Note: Resolving power is also the reciprocal of the limit of resolution of the microscope. Also note that, $RP\propto a$ and $RP\propto \dfrac{1}{\lambda}$. The angular resolution is used to resolve small images into two distinct objects; this is the principle behind the human eye, telescope, microscope, and cameras. However the criterion has minor changes with respect to different optical tools used.