Question

If f is defined on an interval [a,b], which of the following is/are incorrect:
[a] If f(a) and f(b) are of opposite sign, then there must exist a point c in (a,b) such that f(c) = 0
[b] If f is continuous on [a,b], $f\left( a \right)<0$ and $f\left( b \right)<0$, then there must exist a point c in (a,b) such that f(x) = 0
[c] If f is continuous on [a,b] and there is a point c in (a,b) such that f(c) = 0, the f(a) and f(b) must be of opposite sign.
[d] If f has no zeros on [a,b], then f(a) and f(b) have the same sign

Answer 1

Hint: Use Intermediate value theorem in option [b]. In option [a] take $f\left( x \right)=\dfrac{1}{x}$ and a = -1 and b = 1. Hence argue that the statement is incorrect. For option [c] take $f\left( x \right)={{x}^{2}}$ and a =-1, b = 1 and c= 0. Hence argue why the statement is incorrect. For option [d] again take $f\left( x \right)=\dfrac{1}{x}$ and a = -1 and b = 1. Hence argue that the statement is incorrect.

Complete step-by-step answer:
When we prove that a statement is correct, we need to come up with formal proof, and when we prove that a statement is incorrect, we come with a counterexample(Proof by counterexample).
In the question above, we will argue that the statements a,c and d are incorrect, whereas statement b is correct. We will come up with counterexamples disproving statements a,c and d and we will prove the correctness of the statement in option [b].
Proving that statement [a] is incorrect:
Consider the function $f\left( x \right)=\dfrac{1}{x}$, in the interval $\left[ -1,1 \right]$.
We have $f\left( -1 \right)=-1<0$ and $f\left( 1 \right)=1>0$.
However if f(x) = 0, we have 1 = 0, which is not possible.
Hence we have f(1), and f(-1) have opposite signs, but there exists no c in (-1,1) such that f(c) = 0. Hence the given statement is incorrect.
Proving the correctness of statement [b]:
Intermediate Value theorem: According to intermediate value theorem if f(x) is a continuous function in the interval [a,b], then for all $y$ lying between f(a) and f(b), there exists $c\in \left( a,b \right)$ such that $f\left( c \right)=y$.
Since f is continuous in the interval $\left[ a,b \right]$ and $f\left( a \right)<0,f\left( b \right)>0$, we have $0\in \left( f\left( a \right),f\left( b \right) \right)$
Hence by Intermediate Value theorem, there exists $c\in \left( a,b \right)$ such that f(c) = 0. Hence the statement is correct.
Proving that the statement [c] is incorrect:
Consider $f\left( x \right)={{x}^{2}}$.
Since f(x) is a polynomial and since every polynomial is continuous in $\mathbb{R}$, we have f(x) is continuous in the interval [-1,1].
Clearly, there exists $c=0\in \left( -1,1 \right)$ such that $f\left( c \right)=0$, but $f\left( 1 \right)>0$ and $f\left( -1 \right)>0$ and hence f(1) and f(-1) have the same sign.
Hence statement [c] is incorrect.
Proving that the statement [d] is incorrect:
Consider $f\left( x \right)=\dfrac{1}{x}$.
Clearly, f(x) has no zeros in $\mathbb{R}$ , and hence f(x) has no zeros in $\left[ -1,1 \right]$. But $f\left( 1 \right)>0$ and $f\left( -1 \right)>0$ and hence have opposite signs. Hence option [d] is incorrect.
Hence only options [a],[c] and [d] are incorrect.

Note:[1] Visualising graphically:
Graph of $f\left( x \right)=\dfrac{1}{x}$

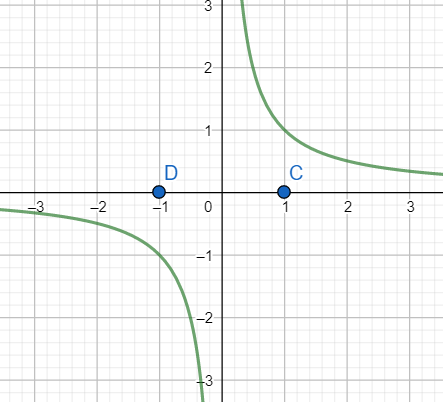
As is evident from the graph that in the interval [C, D] f(x) takes both negative values, but has no zeros. Hence options [a] and [d] are incorrect.

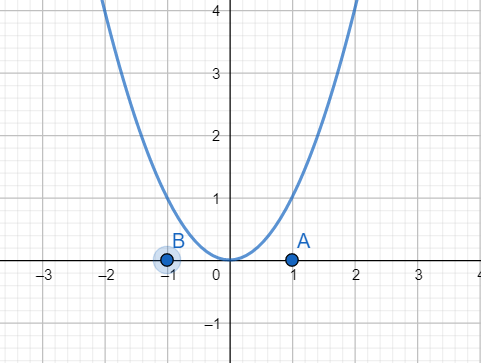
As evident from the graph of $f\left( x \right)={{x}^{2}}$, that f(A) and f(B) are of the same sign. But there exists a root of f(x) in the interval [B, A]
When we draw a continuous graph from x = a to x = b, our hand should not get raised from the paper while plotting. In other words, we can draw a continuous graph, not raising our hand until the graph is complete. Now if f(a) and f(b) are of opposite signs, (a,f(a)) and (b,f(b)) are on opposite sides of the x-axis, and hence when we draw the graph we need to cross the x-axis at least once in the interval (a,b) since we cannot raise our hand(Try it yourself once) and hence there exists c in the interval (a,b) such that f(c) = 0, which proves the statement [b] is correct.