Question

If f, e and v represent the number of rectangular faces, number of edges and number of vertices respectively of cuboid then the value of f + e + v is
A) 20
B) 26
C) 30
D) 18

Answer 1

Hint: From the diagram of the cuboid we can calculate f, e and v denoting number of faces, edges and vertices:
Faces: The rectangles constituting cuboid are its faces
Edges: Line segment between adjacent vertices
Vertices: Point of intersection of two edges.

Complete step-by-step answer:
Figure of a cuboid is:

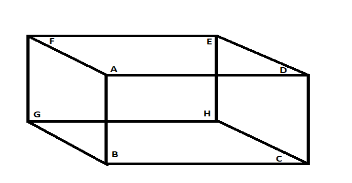
i) Number of rectangular faces (f) are :
1. ABCD
2. ADEF
3. FGBA
4. DEHC
5. GBCH
6. FGHE
f = 6
ii) Number of edges (e) are :
1. FA
2. AD
3. DE
4. EF
5. FG
6. AB
7.GB
8. BC
9. HC
10. CD
11.HE
12. GH
e = 12
iii) Number of vertices (v) are :
1. A
2. B
3. C
4. D
5. E
6. F
7. G
8. H
v = 8
Now, according to the question:
f + e + v = ?
Substituting the calculated values, we get:
f + e + v = 6 + 12 + 8
f + e + v = 26
therefore, if f, e and v represent the number of rectangular faces, number of edges and number of vertices respectively of cuboid then the value of f + e + v is 26
So, the correct answer is “Option B”.

Note: When the faces are written they are always written is adjacent order
e.g. ABCD is right but ACBD is not.
The faces of cuboids are parallel but different in dimensions and when these dimensions are equal, it becomes a cuboid.