Question

If events A and B are independent and $P\left( A \right)=0.15,P\left( A\cup B \right)=0.45$ then $P\left( B \right)=$
(a)$\dfrac{6}{13}$
(b)$\dfrac{6}{17}$
(c)$\dfrac{6}{19}$
(d)$\dfrac{6}{23}$

Answer 1

Hint: Two events A and B will be independent events of the relation between $P\left( A \right)$ and $P\left( B \right)$ is given as $P\left( A\cap B \right)=P\left( A \right)P\left( B \right)$ .
Now, use the relation among $P\left( A \right),P\left( B \right),P\left( A\cap B \right)$ and $P\left( A\cup B \right)$, which is given as:
$P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$ .
Now, put all the known values to the above equation to get the value of $P\left( B \right)$ .

Complete step-by-step answer:
Here, we are given that A and B are two independent events with the relations
$P\left( A \right)=0.15$ ………………… (1)
$P\left( A\cup B \right)=0.45$………………. (2)
And hence, we need to determine the value of $P\left( B \right)$.
Now, as we know A and B can be two independent events if:
$P\left( A\cap B \right)=P\left( A \right)P\left( B \right)$………………………………. (3)
And also, we know the relation among $P\left( A \right),P\left( B \right),P\left( A\cap B \right)$ and $P\left( A\cup B \right)$is given :
$P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$…………………. (4)
Now, we can use equations (1), (2), (3) to put the values of $P\left( A \right),P\left( A\cup B \right)$ and $P\left( A\cap B \right)$ to the equation (4) . So, we get the equation (4) as :
$0.45=0.15+P\left( B \right)-P\left( A \right)P\left( B \right)$
As, we know $P\left( A \right)=0.15$from the equation (1) , so, we can rewrite the above equation as:
$0.45=0.15+P\left( B \right)-0.15P\left( B \right)$
Or
$\begin{align}
  & 0.45-0.15=P\left( B \right)-0.15P\left( B \right) \\
 & 0.30=P\left( B \right)-0.15P\left( B \right) \\
\end{align}$
Now, we can take $P\left( B \right)$ as common from both the terms of the right hand side of the above equation. So, we get $0.30=P\left( B \right)\left( 1-0.15 \right)$
Or
$0.30=P\left( B \right)\times 0.85$
On dividing the above equation by 0.85, we get:
$\dfrac{0.30}{0.85}=P\left( B \right)\times \dfrac{0.85}{0.85}$
Or $P\left( B \right)=\dfrac{0.30}{0.85}$
On multiplying the denominator and numerator by 100, we get:
$\begin{align}
  & P\left( B \right)=\dfrac{0.30}{0.85}\times \dfrac{100}{100}=\dfrac{30}{85} \\
 & P\left( B \right)=\dfrac{6}{17} \\
\end{align}$
Hence, we get $P\left( B \right)=\dfrac{6}{17}$ . So, option (b) is the correct answer of the problem.

Note: One may use Venn diagram for the relation $P\left( A \right)$ and $P\left( B \right)$ as:

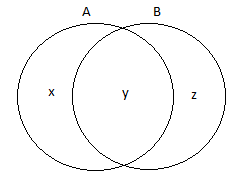
$\begin{align}
  & x+y=P\left( A \right) \\
 & y+z=P\left( B \right) \\
 & y=P\left( A\cap B \right) \\
 & x+y+z=P\left( A\cup B \right) \\
\end{align}$
Writing $P\left( A\cap B \right)=P\left( A \right)P\left( B \right)$ is the key point of the problem as A and B are independent events i.e. events A or B are not depending on each other.