Question

If each side of an equilateral triangle is tripled then what is the percentage increase in the area of the triangle?

Answer 1

Hint: Assume the length of each side of the initial equilateral triangle as a and that of the new equilateral triangle as a’. First find the value of a’ by multiplying a with 3. Now, find the increase in the numerical value of the area by subtracting the area of original triangle from the area of the new triangle using the relation $\left( \dfrac{\sqrt{3}}{4}{{\left( a' \right)}^{2}}-\dfrac{\sqrt{3}}{4}{{\left( a \right)}^{2}} \right)$. Now, find the fractional increase in the area by dividing the obtained difference with the area of the original triangle. Finally, multiply the obtained fraction with 100 to get the answer.

Complete step by step solution:
Here we have been asked to find the percentage increase in the area of an equilateral triangle if we increase the length of each of its sides by 3 times. First we need to find the length of the sides of new triangle.
Let us assume the length of each side of the original triangle as a. We know that the area of an equilateral triangle is given by the formula Area = \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\], so we get,

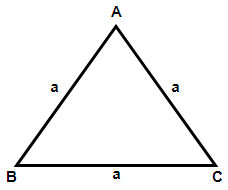
$\Rightarrow $ Area of the original triangle = \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\]
Now, let us assume the length of each side of the new equilateral triangle as a’, it is said that the side is increased 3 times, so mathematically we have the new length of each side given as: -
$\Rightarrow $ a’ = 3a
Therefore using the formula for the area of the triangle in this case we have Area = $\dfrac{\sqrt{3}}{4}{{\left( a' \right)}^{2}}$, so we get,

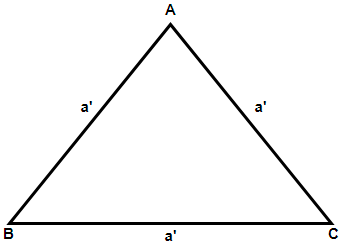
$\Rightarrow $ Area of the new triangle = \[\dfrac{\sqrt{3}}{4}{{\left( 3a \right)}^{2}}\]
$\Rightarrow $ Area of the new triangle = \[\dfrac{9\sqrt{3}}{4}{{a}^{2}}\]
Therefore, fractional increase in the area of the triangle will be the ratio of increase in area of the triangle and the area of the original triangle. So we get,
$\Rightarrow $ Increase in the area = $\left( \dfrac{9\sqrt{3}{{a}^{2}}}{4}-\dfrac{\sqrt{3}}{4}{{a}^{2}} \right)$
$\Rightarrow $ Increase in the area = $8\times \dfrac{\sqrt{3}}{4}{{a}^{2}}$
$\Rightarrow $ Increase in the area = $2\sqrt{3}{{a}^{2}}$
$\Rightarrow $ Fractional increase in the area = $\dfrac{2\sqrt{3}{{a}^{2}}}{\left( \dfrac{\sqrt{3}}{4}{{a}^{2}} \right)}$
Cancelling the common factors we get,
$\Rightarrow $ Fractional increase in the area = $\dfrac{8}{1}$
Therefore, multiplying the above fraction with 100 we get the percentage increase as: -
$\Rightarrow $ Percentage increase in the area = $\dfrac{8}{1}\times 100$
$\therefore $ Percentage increase in the area = 800
Hence, the percentage increase in the area of the equilateral triangle is 800%.

Note: Always remember that the percentage increase or decrease is calculated upon the initial expression and not the final expression. You can also use the Heron’s formula to get the answer. According to this formula Area of any triangle is given as $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ where s is the semi perimeter given as $s=\dfrac{a+b+c}{2}$ and a, b and c are the sides opposite to the angles A, B and C respectively of the triangle.