Question

If each side of an equilateral triangle is $ 4\sqrt{3}cm $ then which of the following is/are true?
a. If area is natural number
b. Numerical value of area and perimeter are same/equal
c. Perimeter is an irrational number
d. All of these are correct

Answer 1

Hint:T In order to find the solution of this question, we will find the perimeter and area of the triangle by the formula, perimeter = $ 3\times \text{side} $ and area = $ \dfrac{\sqrt{3}}{4}{{\left( \text{side} \right)}^{2}} $ . And then we will consider each option one by one and check which of them is/are correct.

Complete step-by-step answer:
In this question, we have been given an equilateral triangle of side $ 4\sqrt{3}cm $ and we have been asked which of the given options is/are true. To solve this question, let us first visualize the figure and draw the diagram accordingly for better understanding. So, we get,

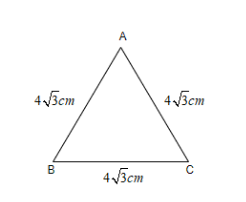
Now, we know that the area of an equilateral triangle is given by $ \dfrac{\sqrt{3}}{4}{{\left( \text{side} \right)}^{2}} $ . And we know that the side of triangle ABC is $ 4\sqrt{3}cm $ . So, we can say,
Area of triangle ABC = $ \dfrac{\sqrt{3}}{4}{{\left( 4\sqrt{3} \right)}^{2}} $
Now, we will simplify it further to get the answer. So, we get,
Area of triangle ABC = $ \dfrac{\sqrt{3}}{4}\times 16\times 3 $
Area of triangle ABC = $ 12\sqrt{3}c{{m}^{2}} $
Now, let us calculate the perimeter of the equilateral triangle. We know that the perimeter of an equilateral triangle is calculated as, $ 3\times \text{side} $ . And we know that the side of triangle ABC = $ 4\sqrt{3}cm $ . So, we can say,
Perimeter of triangle ABC = $ 3\left( 4\sqrt{3} \right) $
Perimeter of triangle ABC = $ 12\sqrt{3}cm $
Now, we will consider each option one by one. So, let us take option (a), that area is the natural number.
Now, we know that natural numbers are like, 1, 2, 3, 4, …… Now, we know that area of triangle ABC is $ 12\sqrt{3}c{{m}^{2}} $ , which is definitely not a natural number. So, we can say area of is not a natural number. So, option (a) is the wrong option.
Now, let us take option (b), that is, the numerical value of perimeter and area are same and equal.
From the formula of perimeter and the formula of area, we have received the perimeter of triangle ABC as $ 12\sqrt{3}cm $ and the area of triangle ABC as $ 12\sqrt{3}c{{m}^{2}} $ . Here, we can see that the only difference in both the values is the difference of units. So, we can say that the numerical values of perimeter and area are the same. Therefore, option (b) is the correct option.
Now, let us consider option (c), that is, perimeter is an irrational number.
We have got the perimeter of the triangle as $ 12\sqrt{3}cm $ . Now, we know that $ \sqrt{3} $ is an irrational number. So, we can say that $ 12\sqrt{3} $ is an irrational number. Therefore, we can say that the perimeter is an irrational number. So, option (c) is a correct option.
Now, we will consider option (d), that is, all of these are correct.
We have seen that option (a) is wrong but options (b) and (c) are correct. So, we cannot say that all the options are correct. Hence, option (d) is wrong.
So, from all the above observations, we can say that options (b) and (c) are the correct options.

Note: While solving this question, we can find the area of triangle ABC by using the formula, $ \dfrac{1}{2} $ (base) (height), where base will be any of the sides height will be the respective altitude. And we know that it can be a lengthy method to find the area of the triangle. So, we might waste our time while solving the question using this method. So, it is better to apply the formula, area = $ \dfrac{\sqrt{3}}{4}{{\left( \text{side} \right)}^{2}} $ for finding the area of the given equilateral triangle.