Question

If each side of a triangle is double, then find the ratio of area of the new triangle thus formed and the given triangle.
A. 4:1
B. 1:4
C. 2:1
D. 1:2

Answer 1

Hint- In this question, first we consider a triangle with its three sides are a, b and c respectively. And find its semi-perimeter and with the help of Heron’s formula, we will calculate its area. And then after each side of a triangle is double i.e. sides of a new triangle will be 2a,2b,2c. and also we will calculate the area of the new triangle with new sides and take its ratio.

Complete step-by-step answer:
Semi perimeter of the triangle (s) = $\dfrac{{{\text{a + b + c}}}}{{\text{2}}}$
Area of triangle (A) = $\sqrt {{\text{s}}\left( {{\text{s - a}}} \right)\left( {{\text{s - b}}} \right)\left( {{\text{s - c}}} \right)} $ ………. (Heron’s formula)

As given in question,
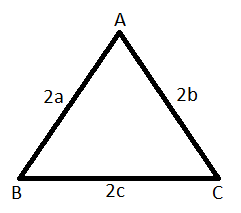
If each sides of a triangle is double i.e.
Sides of the new triangle will be 2a,2b,2c.
Semi perimeter of the new triangle = $\dfrac{{{\text{2a + 2b + 2c}}}}{{\text{2}}}$ = $\dfrac{{{\text{a + b + c}}}}{1}$
                                                                                          = 2s
Now, the area of the new triangle is calculated.
Area of the new triangle = $\sqrt {{\text{2s}}\left( {{\text{2s - 2a}}} \right)\left( {{\text{2s - 2b}}} \right)\left( {{\text{2s - 2c}}} \right)} $
                                            = $\sqrt {{{\text{2}}^{\text{4}}}{\text{s}}\left( {{\text{s - a}}} \right)\left( {{\text{s - b}}} \right)\left( {{\text{s - c}}} \right)} $
                                            = ${2^2}$$\sqrt {{\text{s}}\left( {{\text{s - a}}} \right)\left( {{\text{s - b}}} \right)\left( {{\text{s - c}}} \right)} $
                                            = 4 A
                                           = 4 x area of the original triangle.
Hence, the ratio of area of the new triangle thus formed and the given triangle is 4:1.
So, option (A) is the correct answer.
Note-If base and height of a triangle are given in the question, then in this case we need to use formula for Area of a triangle is-
Area of a triangle = $\dfrac{1}{2}$ × Base × Height