Question

If each side of a scalene triangle is tripled then prove that ratio of their area will be 1:9.

Answer 1

Hint: Consider a scalene triangle $ \Delta AHE $ and extend its sides to get another scalene $ \Delta AMT $ with sides three times of $ \Delta AHE $ . Now use the property that the area of a triangle is half of the product of the length of two sides of the triangle with the sine of the angle between these two sides.

Complete step-by-step answer:
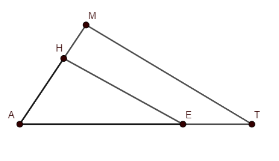
To start with the question, let us Consider a scalene triangle $ \Delta AHE $ and extend its sides to get another scalene $ \Delta AMT $ with sides three times of $ \Delta AHE $ . Let us draw a rough diagram for better understanding.

As we have taken the side of $ \Delta AMT $ to be three times of $ \Delta AHE $ .
 $ \therefore \dfrac{MA}{HA}=\dfrac{AT}{AE}=\dfrac{TM}{EH}=3............(i) $
Also, $ \angle MAT=\angle HAE.............(ii) $ .
Now we know that the area of a triangle is half of the product of the length of two sides of the triangle with the sine of the angle between these two sides.
 $ \therefore ar\left( \Delta AMT \right)=\dfrac{1}{2}\times MA\times TM\times \sin \left( \angle MAT \right) $
 $ \therefore ar\left( \Delta AHE \right)=\dfrac{1}{2}\times HA\times EH\times \sin \left( \angle HAE \right) $
Now we will find the ratio of the areas of the two triangle.
 $ \therefore \dfrac{ar\left( \Delta AMT \right)}{ar\left( \Delta AHE \right)}=\dfrac{\dfrac{1}{2}\times MA\times TM\times \sin \left( \angle MAT \right)}{\dfrac{1}{2}\times HA\times EH\times \sin \left( \angle HAE \right)}=\dfrac{MA}{HA}\times \dfrac{TM}{EH}\times \dfrac{\sin \left( \angle AMT \right)}{\sin \left( \angle AHE \right)} $
Now if we substitute the values of $ \dfrac{MA}{HA}\text{ and }\dfrac{TM}{EH} $ from equation (i), we get
 $ \therefore \dfrac{ar\left( \Delta AMT \right)}{ar\left( \Delta AHE \right)}=3\times 3\times \dfrac{\sin \left( \angle MAT \right)}{\sin \left( \angle HAE \right)} $
Also, from equation (ii), we know $ \angle MAT=\angle HAE $ , so their sine would also be the same.
 $ \therefore \dfrac{ar\left( \Delta AMT \right)}{ar\left( \Delta AHE \right)}=\dfrac{3\times 3}{1}=\dfrac{9}{1} $

Therefore, we have shown that if each side of a scalene triangle is tripled then prove that the ratio of their area will be 1:9.

Note: If you have notices that the triangles $ \Delta AMT $ and $ \Delta AHE $ are similar triangles as each side is made thrice so the ratio of new sides to the corresponding old side is equal to 3:1, which is constant and satisfies the criteria of similar triangles. If you want, you can solve the question using the heron’s formula of area of a triangle as well, but that would be a bit lengthier.