Question

If each pair of sides of a quadrilateral is equal, then prove that it is a parallelogram.

Answer 1

Hint: To solve this question, we will make a quadrilateral and join its opposite corners with a diagonal. Then the triangles formed due to this diagonal have one side common, and then we will prove that these triangles are congruent. After proving their congruence, we will equate the corresponding angles by CPCT (corresponding parts of congruent triangles). Then, with the help of these, we will compare this quadrilateral with the parallelogram.

Complete step-by-step answer:
Before solving the question, we must know what a parallelogram is. A parallelogram is a quadrilateral in which the opposite sides are parallel and equal to each other. Now, it is given in question that the opposite sides are equal. We have to prove that opposite sides will be parallel also. For this, we will make a quadrilateral ABCD and then we will construct a diagonal.

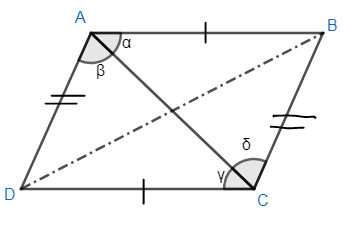
From the above quadrilateral, we can see that $AB=CD$ and $AD=BC$ . Now, from the triangles ABC and ADC, we have:
$AD=BC$ (given) (b)
$AB=CD$ (given) (b)
$AC=AC$ (common side) (b)
Thus the triangle ABC is congruent to the triangle ACD. Now, we know that if two triangles are congruent then the corresponding angles will be equal by CPTC. So, we can say that:
$\alpha =\gamma $ (By CPCT)
$\beta =\sigma $ (By CPCT)
Now, if $\alpha =\gamma $, we can say that the lines AB and CD are parallel because $\alpha $ and $\gamma $ will be the alternate interior angles. Similarly, if $\beta =\sigma $, we can say that lines AD and BC will parallel. Thus, we have:
$AB=CD,AD=BC,AB\parallel CD\text{ and }AD\parallel BC$
Thus, the quadrilateral given is a parallelogram.
Hence, proved.

Note: We can also prove the above theorem as follows:
We know that $\Delta ABC$ is congruent to $\Delta ADC$ . So, by CPCT, we have:
 $\angle ABC=\angle ADE$ ……………………. (1)
Similarly, the triangles ABD and BCD will also be congruent. So, by CPCT, we can say that :
$\angle DAB=\angle DCB$ ………………….. (2)
Now, we know that the sum of interior angles in a quadrilateral is 360. Thus,
$\begin{align}
  & \angle ABC+\angle ADE+\angle DAB+\angle DCB={{360}^{\circ }} \\
 & 2\angle ABC+2\angle DCB={{360}^{\circ }} \\
 & \angle ABC+\angle DCB={{180}^{\circ }} \\
\end{align}$
Now, if the sum of interior angles is $180{}^\circ $ then lines will be parallel. So, $AB\parallel CD.$