Question

If \[\dfrac{{\tan 3\theta }}{{\tan \theta }} = 4\] , then \[\dfrac{{\sin 3\theta }}{{\sin \theta }}\] equals:
(A) \[\dfrac{8}{3}\]
(B) \[\dfrac{4}{5}\]
(C) \[\dfrac{3}{4}\]
(D) None of these

Answer 1

Hint:
According to the question, use the formula \[\tan 3\theta = \dfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }}\] and simplify to get the value of \[\tan \theta \] and calculate the value in terms of sin to find the required answer. Then again use the formula of \[\sin 3\theta = 3\sin \theta - 4{\sin ^3}\theta \] to find the value of \[\dfrac{{\sin 3\theta }}{{\sin \theta }}\].

Formula used:
Here, we use the trigonometric formulas that is \[\tan 3\theta = \dfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }}\] and \[\sin 3\theta = 3\sin \theta - 4{\sin ^3}\theta \].

Complete step by step solution:
As it is given, \[\dfrac{{\tan 3\theta }}{{\tan \theta }} = 4\]
Take \[\tan \theta \] on the right hand side in multiply.
So we get, \[\tan 3\theta = 4\tan \theta \]
Here, we will use the formula of \[\tan 3\theta = \dfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }}\]
On substituting we get,
\[\dfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }} = 4\tan \theta \]
Taking \[\tan \theta \] common in numerator from right hand side,
\[\dfrac{{\tan \theta \left( {3 - {{\tan }^2}\theta } \right)}}{{1 - 3{{\tan }^2}\theta }} = 4\tan \theta \]
Cancelling \[\tan \theta \] from both right hand side and left hand side,
So we get,
\[\dfrac{{3 - {{\tan }^2}\theta }}{{1 - 3{{\tan }^2}\theta }} = 4\]
Taking denominator of left hand side to the right hand side,
\[3 - {\tan ^2}\theta = 4(1 - 3{\tan ^2}\theta )\]
\[3 - {\tan ^2}\theta = 4 - 12{\tan ^2}\theta \]
After simplifying we get,
\[ - {\tan ^2}\theta + 12{\tan ^2}\theta = 4 - 3\]
\[11{\tan ^2}\theta = 1\]
So, \[{\tan ^2}\theta = \dfrac{1}{{11}}\]
After taking square root on both side we get,
\[\tan \theta = \sqrt {\dfrac{1}{{11}}} \]
As we know \[\sqrt 1 = 1\] and \[\sqrt {11} = \sqrt {11} \]
Substituting all the calculated values we get,
\[\tan \theta = \dfrac{1}{{\sqrt {11} }}\]
As we know \[\tan \theta = \dfrac{{Perpendicular}}{{Base}}\]
So, we will draw a right angled triangle \[\Delta ABC\] having angle \[\theta \] , base \[ = \sqrt {11} \] and perpendicular = 1 as shown in figure.

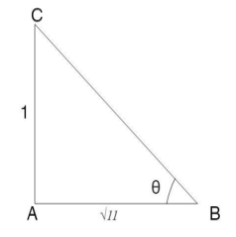
As of now we will calculate Hypotenuse by using the Pythagoras theorem that is \[{H^2} = {P^2} + {B^2}\]
So, we will substitute all the values of P and B to get the value of H .
In right angled triangle \[\Delta ABC\]
\[{H^2} = {1^2} + {\left( {\sqrt {11} } \right)^2}\]
After calculating squares we get,
\[{H^2} = 1 + 11\]
\[{H^2} = 12\]
After taking square root on both side we get,
\[H = \sqrt {12} = 2\sqrt 3 \]
So, now we will calculate \[\sin \theta = \dfrac{P}{H}\]
Putting P = 1 and \[H = 2\sqrt 3 \] we get,
\[\sin \theta = \dfrac{1}{{2\sqrt 3 }}\]
As, according to the question we have to calculate \[\dfrac{{\sin 3\theta }}{{\sin \theta }}\]
Here, we use the formula of \[\sin 3\theta = 3\sin \theta - 4{\sin ^3}\theta \]
After substituting we get,
\[ \Rightarrow \dfrac{{3\sin \theta - 4{{\sin }^3}\theta }}{{\sin \theta }}\]
Taking \[\sin \theta \] common from numerator and cancelling \[\sin \theta \] from numerator and denominator we get,
\[ \Rightarrow 3 - 4{\sin ^2}\theta \]
Putting the value of \[\sin \theta = \dfrac{1}{{2\sqrt 3 }}\] in the above equation.
\[ \Rightarrow 3 - 4{\left( {\dfrac{1}{{2\sqrt 3 }}} \right)^2}\]
On simplifying we get,
\[ \Rightarrow 3 - \dfrac{1}{3}\]
By taking L.C.M we get,
\[ \Rightarrow \dfrac{8}{3}\]

So, option (A) \[\dfrac{8}{3}\] is correct.

Note:
To solve these types of questions, you must remember the trigonometric formulas and conversion of trigonometric values. For conversion you can simply use Pythagoras theorem to find the required value.