
If \[\Delta ABC\sim \Delta EDF\] and \[\Delta ABC\] is not similar to \[\Delta DEF\], then which of the following is not true?
\[\begin{align}
& \left( A \right)BC.EF=AC.FD \\
& \left( B \right)AB.EF=AC.DE \\
& \left( C \right)BC.DE=AB.EF \\
& \left( D \right)BC.DE=AB.FD \\
\end{align}\]
Answer
524.1k+ views
Hint: In order to check out which of the mentioned is false, we will be showing the triangles as similar using the SSS property and then we will be showing the angles are equal or not. After obtaining all the properties, we will be checking out for each of the given options.
Complete step-by-step solution:
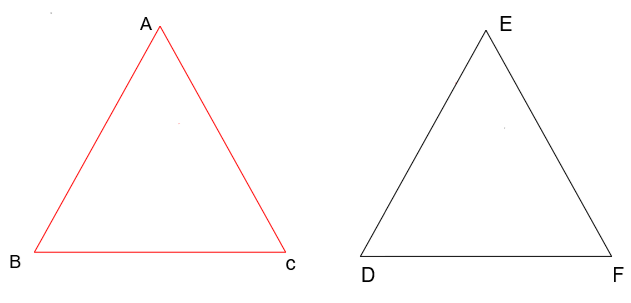
Now let us learn about the similarities of the triangle. We can say that two triangles are similar if two pairs of corresponding angles in a pair of triangles are congruent, then the triangles are similar. We know that if two angle pairs are the same , then the third angle will also be the same. When the three angle pairs are all equal, the three pairs of sides must also be in proportion.
Now let us start solving the problem.
As per the SSS Similarity rule of similar triangles, sides of both the triangles are proportional to each other, which makes their angles also equal.
\[\Delta ABC\sim \Delta DEF\]
\[\Rightarrow \dfrac{AB}{ED}=\dfrac{BC}{DF}=\dfrac{AC}{EF}\]
Upon considering the similarity property, we obtain
\[\dfrac{AB}{ED}=\dfrac{BC}{DF}\]
\[\Rightarrow AB.DF=BC.ED\]
According to this, option D is true.
Upon considering the last two terms, we get
\[\dfrac{BC}{DF}=\dfrac{AC}{EF}\]
\[\Rightarrow BC.EF=AC.DF\]
We can conclude that option A is true according to this.
Now consider the first and the last term i.e. \[\dfrac{AB}{ED}=\dfrac{AC}{EF}\]
\[\Rightarrow AB.EF=AC.ED\]
We can say that option B is also true.
Option C could not be proven true from any of the considerations, therefore, option C is not true regarding the given similarity of the triangles.
Note: The main error could occur when we try to prove the triangles using other similarity theorems without considering the given factors. We can also check the angles, if they are equal, then we can say that triangles are similar.
Complete step-by-step solution:
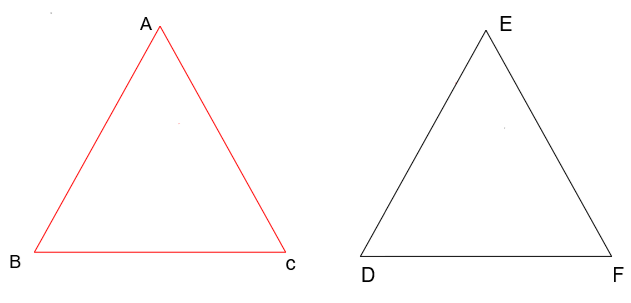
Now let us learn about the similarities of the triangle. We can say that two triangles are similar if two pairs of corresponding angles in a pair of triangles are congruent, then the triangles are similar. We know that if two angle pairs are the same , then the third angle will also be the same. When the three angle pairs are all equal, the three pairs of sides must also be in proportion.
Now let us start solving the problem.
As per the SSS Similarity rule of similar triangles, sides of both the triangles are proportional to each other, which makes their angles also equal.
\[\Delta ABC\sim \Delta DEF\]
\[\Rightarrow \dfrac{AB}{ED}=\dfrac{BC}{DF}=\dfrac{AC}{EF}\]
Upon considering the similarity property, we obtain
\[\dfrac{AB}{ED}=\dfrac{BC}{DF}\]
\[\Rightarrow AB.DF=BC.ED\]
According to this, option D is true.
Upon considering the last two terms, we get
\[\dfrac{BC}{DF}=\dfrac{AC}{EF}\]
\[\Rightarrow BC.EF=AC.DF\]
We can conclude that option A is true according to this.
Now consider the first and the last term i.e. \[\dfrac{AB}{ED}=\dfrac{AC}{EF}\]
\[\Rightarrow AB.EF=AC.ED\]
We can say that option B is also true.
Option C could not be proven true from any of the considerations, therefore, option C is not true regarding the given similarity of the triangles.
Note: The main error could occur when we try to prove the triangles using other similarity theorems without considering the given factors. We can also check the angles, if they are equal, then we can say that triangles are similar.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




