Question

If \[\Delta ABC\] and \[\Delta AMP\] are right triangles, right-angled at B and M respectively and
\[\angle MAP=\angle BAC\]
Prove that
\[\begin{align}
  & \left( a \right)\Delta ABC\sim \Delta AMP \\
 & \left( b \right)\dfrac{CA}{PA}=\dfrac{BC}{MP} \\
\end{align}\]

Answer 1

Hint: In this question, first draw the diagram it will give us a clear picture of how we can prove the given conditions. List all the conditions required to prove similarity and they are given \[\angle MAP=\angle BAC\], Using these try to get a relation out of that.

Complete step-by-step answer:
Let us first draw the diagrams accordingly and then observe them.

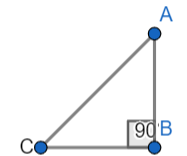
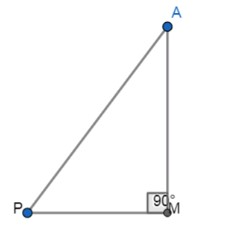
It is given that \[\angle MAP=\angle BAC\].
Now, let us know about some basic definitions.
Angle: If two rays are drawn in different directions from a common initial point, then they are said to form an angle.

Triangle: A figure bounded by three line segments in a plane is called a triangle. It has three vertices, three sides and three angles.
Right Angled Triangle: A triangle having one of the angles measures \[{{90}^{\circ }}\] is called a right angled triangle.

Congruent angles: Two angles are said to be congruent if they are equal.
Similarity of Triangles:
Two triangles are said to be similar, if they are alike in shape only and it is denoted by the symbol \[\left( \sim \right)\]. The corresponding angles of two similar triangles are equal but the corresponding sides are only proportional but not equal. Two triangles are similar, if
The three angles of one triangle are respectively equal to the three angles of the second triangle (AAA).
Two sides of one triangle are proportional to two sides of the other and the included angles are equal (SAS).
The corresponding sides of two triangles are in the same ratio then triangles are similar (SSS).
\[\text{As }\angle MAP=\angle BAC\text{ and }\angle B=\angle M={{90}^{\circ }}\]
Now, from the given conditions we know that,
\[\angle MAP=\angle BAC\]
\[\angle B=\angle M={{90}^{\circ }}\]
As two angles are equal it implies that the third angle in both the triangles is also equal.
So, from the above AAA similarity we can say that both the given triangles are similar.
\[\therefore \Delta ABC\sim \Delta AMP\].
Now, as we know that both the triangles are similar we can say that from SAS similarity the two sides of one triangle are proportional to the two sides of the other triangle because the included angles are equal.
\[\text{As }\angle MAP=\angle BAC\text{ and }\angle B=\angle M={{90}^{\circ }}\]
We can say that,
 \[\angle ACB=\angle APM\]
\[\therefore \dfrac{CA}{PA}=\dfrac{BC}{MP}\]

NOTE: It is important to observe that the corresponding angles of the given triangles are congruent. So, we can accordingly establish the corresponding similarity AAA because if two angles in both the triangles are equal then we can say that the third angle must be equal.
 While showing that the two sides are proportional for the two triangles we need to keep in mind that we already established the relation between the angles for the two triangles which imply that the included angles are equal in both of them.
We should use SAS similarity to show the proportion of the sides instead of using the SSS similarity.