Question

If D $ \left( -\dfrac{1}{5},\dfrac{5}{2} \right) $ , E $ (7,3) $ and F $ \left( \dfrac{7}{2},\dfrac{7}{2} \right) $ are the mid-points of sides of $ \Delta ABC $ , find the area of $ \Delta ABC $ .

Answer 1

Hint: As we know that to find the area of triangle if coordinates are given of vertices of triangle\[\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}}) \right]\], in which\[\left( {{x}_{1}},{{y}_{1}} \right),({{x}_{2}},{{y}_{2}})\]and $ ({{x}_{3}},{{y}_{3}}) $ are the coordinates of triangle. So we will use the midpoints coordinate of the triangle to find the area of $ \Delta DEF $ , from which we will further multiply by 4 to find the area of $ \Delta ABC $ .

Complete step by step answer:
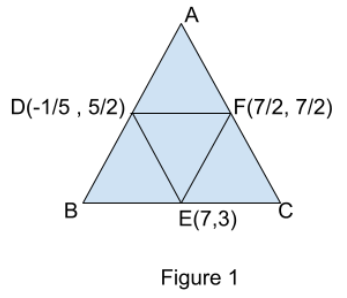
Moving ahead with the question, of triangle $ \Delta ABC $ with mid-point D, E and F as shown in figure 1,
By the mid-point theorem of triangle we know that a triangle formed by joining the mid-points of a triangle, its area will be one fourth of the actual area of the triangle. As in our case we can say that the area of the triangle formed by joining the mid-points D, E and F will be one fourth of the area of the actual triangle.

So in order to find the area of the actual area of the triangle we have to first find out the area of the triangle formed by joining the mid-points of the triangle and then multiply by 4.
So to find out the area of triangle if we know the coordinates will be\[\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}}) \right]\] in which\[\left( {{x}_{1}},{{y}_{1}} \right),({{x}_{2}},{{y}_{2}})\]and $ ({{x}_{3}},{{y}_{3}}) $ are the coordinates of triangle. So area of $ \Delta DEF $ will be\[\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}}) \right]\]in which\[\left( {{x}_{1}},{{y}_{1}} \right),({{x}_{2}},{{y}_{2}})\]and $ ({{x}_{3}},{{y}_{3}}) $ are the coordinates of triangle $ \Delta DEF $ i.e.
 \[\begin{align}
  & \left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{-1}{5},\dfrac{5}{2} \right), \\
 & ({{x}_{2}},{{y}_{2}})=\left( 7,3 \right) \\
 & ({{x}_{3}},{{y}_{3}})=\left( \dfrac{7}{2},\dfrac{7}{2} \right) \\
\end{align}\]
So area of $ \Delta DEF $ will be;
\[\begin{align}
  & \dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}}) \right] \\
 & \dfrac{1}{2}\left[ -\dfrac{1}{5}\left( 3-\dfrac{7}{2} \right)+7\left( \dfrac{7}{2}-\dfrac{5}{2} \right)+\dfrac{7}{2}\left( \dfrac{5}{2}-3 \right) \right] \\
\end{align}\]
Solving it further to find the value of above expression;
 \[\begin{align}
  &= \dfrac{1}{2}\left[ -\dfrac{1}{5}\left( 3-\dfrac{7}{2} \right)+7\left( \dfrac{7}{2}-\dfrac{5}{2} \right)+\dfrac{7}{2}\left( \dfrac{5}{2}-3 \right) \right] \\
 & =\dfrac{1}{2}\left[ -\dfrac{3}{5}+\dfrac{7}{10}+\dfrac{49}{2}-\dfrac{35}{2}+\dfrac{35}{4}-\dfrac{21}{2} \right] \\
 & =\dfrac{1}{2}\left[ \dfrac{-12+14+490-350+175-210}{20} \right] \\
 & =\dfrac{1}{2}\left[ \dfrac{107}{20} \right] \\
\end{align}\]
So the area of $ \Delta DEF $ we got is $ \dfrac{107}{40} $ .
So for Area of triangle $ \Delta ABC $ will get when we multiply the 4 with the area of $ \Delta DEF $
So area of $ \Delta ABC $ equal $ 4\times \Delta DEF $
 $ \Delta ABC=4\times \Delta DEF $
As $ \Delta DEF $ is equal to $ \dfrac{107}{40} $
So write it in above equation, we will get;
 $ \begin{align}
  & \Delta ABC=4\times \Delta DEF \\
 & =\Delta ABC=4\times \left( \dfrac{107}{40} \right) \\
 & =\Delta ABC=\dfrac{107}{10} \\
\end{align} $
So the area of $ \Delta ABC $ is $ \dfrac{107}{10} $ .
Hence the answer is $ \dfrac{107}{10} $ .

Note: To find the area of triangle\[\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}}) \right]\]you can apply this formula in which you can take any point as\[\left( {{x}_{1}},{{y}_{1}} \right),({{x}_{2}},{{y}_{2}})\]and $ ({{x}_{3}},{{y}_{3}}) $ , it is not necessary that you take D as $ ({{x}_{1}},{{y}_{1}}) $ it can be E or F also, but you should go in the clockwise manner to use this formula, as if you take E as first point i.e. $ ({{x}_{1}},{{y}_{1}}) $ then F will be $ ({{x}_{2}},{{y}_{2}}) $ and D will be $ ({{x}_{3}},{{y}_{3}}) $ .