Question

If D is the point on the side AB of \[\vartriangle ABC\] such that \[AD:DB = 3:2\] and E is the point on BC such that \[DE\left\| {AC} \right.\] . Find the ratio of area of \[\vartriangle ABC\] and \[\vartriangle BDE\]

Answer 1

Hint: We are given with two triangles and also the ratio of the sides of the triangle. Now in order to find the ratio of the areas of the triangles we need to prove that the two given triangles are similar. Using any one of the properties of similarity we will show that the triangles are similar and then the ratio of squares of the sides will give the ratio of areas of the triangles.

Complete step by step solution:
First we will note the given data,
D is the point on the side AB of \[\vartriangle ABC\]
Now we will draw the figure of the given geometrical conditions.

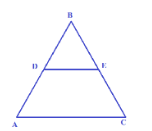
Now we need to show that the triangles are similar.
\[\angle B = \angle B\]……common angle
\[\angle D = \angle A\]……since \[DE\left\| {AC} \right.\] ; these are corresponding angles.
So \[\vartriangle ABC \sim \vartriangle DBE\]…….by AA property
Now since the triangles are similar we can take the respective ratios
Given that \[AD:DB = 3:2\]
That is \[\dfrac{{AD}}{{DB}} = \dfrac{3}{2}\]
But we need the ratio as \[\dfrac{{AB}}{{DB}}\]
So we will add DB to AD to get AB. So we will add one on both the sides.
\[\dfrac{{AD}}{{DB}} + 1 = \dfrac{3}{2} + 1\]
Taking the LCM
\[\dfrac{{AD + DB}}{{DB}} = \dfrac{{3 + 2}}{2}\]
On adding we get,
 \[\dfrac{{AB}}{{DB}} = \dfrac{5}{2}\]
Now taking the square of both sides we will get the ratio of areas.
\[\dfrac{{{{\left( {AB} \right)}^2}}}{{{{\left( {DB} \right)}^2}}} = \dfrac{{25}}{4}\]
Thus ratio of areas of both triangles is given by,
\[\dfrac{{area\left( {ABC} \right)}}{{area\left( {DBE} \right)}} = \dfrac{{25}}{4}\]
This is our final answer.
So, the correct answer is “\[\dfrac{{area\left( {ABC} \right)}}{{area\left( {DBE} \right)}} = \dfrac{{25}}{4}\]”.

Note: Note that in order to find the ratio of areas we need the ratio of the respective sides. Also those two triangles should be similar. If not given their similarity; then we need to use the required properties to show that. In the above case we can take \[\angle C\& \angle E\] as corresponding angles. Also note that the sequence of ration should also be observed. Otherwise though we are correct with our answer we may lose our marks.