Question

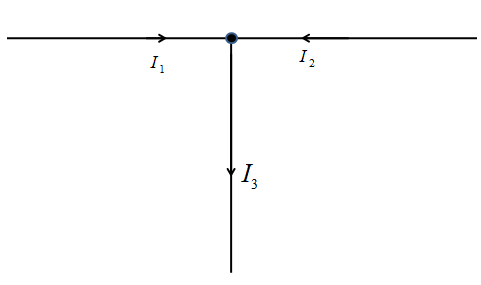
If current ${I_1} = 3A\sin \omega t$ and ${I_2} = 4A\cos \omega t$, then ${I_3}$ is:

Answer 1

Hint: We know that although current has a direction it is not a vector quantity because it does not follow the vector addition law. The addition of current is like the ordinary algebraic addition taking positive or negative. This concept we will use here.

Complete step by step solution:
Two currents are given as below.
${I_1} = 3A\sin \omega t$
${I_2} = 4A\cos \omega t$
We have to calculate the third current. This can be found by Kirchhoff’s junction rule. Which states that the algebraic sum of the currents at the junction will be zero.
So, we can write the following.
${I_1} + {I_2} = {I_3}$
Let us put the values now.
$3A\sin \omega t + 4A\cos \omega t = {I_3}$
So, the third current is given below.
${I_3} = A\left( {3\sin \omega t + 4\cos \omega t} \right)$
Hence, the answer is $A\left( {3\sin \omega t + 4\cos \omega t} \right)$.

Note:
Kirchhoff’s junction rules tell that the algebraic sum of the currents at the junction is zero. This means the current coming to the junction will be equal to the current leaving the junction.
Junction is the node of the circuit where different wires are connected, so current from different directions flows through this point.
We assume the current coming to the junction to be positive and the current leaving the junction to be negative.
When a current flowing in the circuit encounters two paths then it gets divided according to the resistance offered by the path. The path having less resistance will be the path through which maximum current will pass.
If there are two paths, one has some resistance and the other doesn’t then all current will pass through the p[ath having no resistance.
Practically every wire has some resistance called internal resistance.