Question

If \[\cos x=\dfrac{3}{5}\] and \[\cos y=\dfrac{-24}{25}\], where \[\dfrac{3\pi }{2} < x < 2\pi \] and \[\pi < y < \dfrac{3\pi }{2}\], find the value of \[\cos \left( x-y \right)\].

Answer 1

Hint:Find the value of \[\sin x\] and \[\sin y\], by using the trigonometric identity, \[{{\sin }^{2}}x+{{\cos }^{2}}x=1\]. Thus get the value of \[\sin x\] and \[\sin y\] as the values of \[\cos x\] and \[\cos y\] are given. Then substitute in the formula of \[\cos \left( x-y \right)\].

Complete step-by-step answer:
We have been given that, \[\cos x=\dfrac{3}{5}\] and \[\cos y=\dfrac{-24}{25}\]. We need to find the value of \[\cos \left( x-y \right)\].
\[\cos \left( x-y \right)=\cos x\cos y+\sin x\sin y-(1)\]
Hence we need to find the value of \[\sin x\] and \[\sin y\].
So let us find the value of \[\sin x\] first.
We know that, \[{{\sin }^{2}}x+{{\cos }^{2}}x=1\]
We have, \[\cos x=\dfrac{3}{5}\]
\[\begin{align}
  & \therefore {{\sin }^{2}}x+{{\left( \dfrac{3}{5} \right)}^{2}}=1 \\
 & {{\sin }^{2}}x=1-\dfrac{9}{25} \\
 & \sin x=\sqrt{1-\dfrac{9}{25}}=\sqrt{\dfrac{25-9}{25}}=\sqrt{\dfrac{46}{25}}=\pm \dfrac{4}{5} \\
\end{align}\]
Hence, we got the value of \[\sin x\] as \[\left( \pm \dfrac{4}{5} \right)\].
Since x is in IV Quadrant, \[\sin x\] is negative.

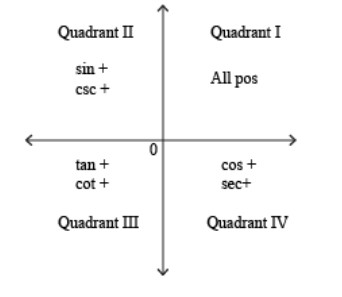
\[\sin x=\dfrac{-4}{5}-(2)\]
Now let us find the value of \[\sin y\] similarly.
\[\begin{align}
  & {{\sin }^{2}}y+{{\cos }^{2}}y=1 \\
 & {{\sin }^{2}}y=1-{{\cos }^{2}}y=1-{{\left( \dfrac{-24}{25} \right)}^{2}} \\
 & {{\sin }^{2}}y=1-\dfrac{{{24}^{2}}}{{{25}^{2}}} \\
 & \therefore \sin y=\sqrt{1-\dfrac{{{24}^{2}}}{{{25}^{2}}}}=\sqrt{\dfrac{625-576}{625}}=\sqrt{\dfrac{49}{625}}=\pm \dfrac{7}{25} \\
\end{align}\]
Now, y lies in IV quadrant, thus \[\sin y\] is negative.
\[\therefore \sin y=\dfrac{-7}{25}-(3)\]
Thus put values of (2) and (3) in (1).
\[\begin{align}
  & \cos \left( x-y \right)=\cos x\cos y+\sin x\sin y \\
 & \cos \left( x-y \right)=\dfrac{3}{5}\times \left( \dfrac{-24}{25} \right)+\left( \dfrac{-4}{5} \right)\times \left( \dfrac{-7}{25} \right) \\
 & \cos \left( x-y \right)=\dfrac{3}{5}\times \dfrac{-24}{25}+\dfrac{4}{5}\times \dfrac{7}{25} \\
 & \cos \left( x-y \right)=\dfrac{-72+28}{125}=\dfrac{-44}{125} \\
\end{align}\]
Hence we got the value of \[\cos \left( x-y \right)=\dfrac{-44}{125}\].

Note: To solve this particular question, you need to know the formula of \[\cos \left( x-y \right)\] otherwise you won’t be able to solve it. After finding the value of \[\sin x\] and \[\sin y\], find its sign by using the quadrant.
Learn the given graph and if you know the quadrants to which the functions belong, you can find the signs of the functions easily. Hence, remember to learn the identities and the trigonometric functions in quadrant.