Question

If $ \cos \theta =\dfrac{2}{3} $ , then $ 2{{\sec }^{2}}\theta +2{{\tan }^{2}}\theta -7 $ is equal to:
A. 1
B. 0
C. 3
D. 4

Answer 1

Hint: First of all apply the trigonometric identity $ 1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta $ in the given expression. Convert the given expression in terms of $ {{\sec }^{2}}\theta $ . Now, it is given that $ \cos \theta =\dfrac{2}{3} $ and we know that the reciprocal of $ \cos \theta $ is $ \sec \theta $ and then substitute the value of $ \sec \theta $ in the given expression and solve.

Complete step-by-step answer:
The expression given in the question is:
 $ 2{{\sec }^{2}}\theta +2{{\tan }^{2}}\theta -7 $
Now, we are going to convert the above expression in terms of $ \sec \theta $ using the trigonometric identity:
 $ \begin{align}
  & 1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta \\
 & \Rightarrow {{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1 \\
\end{align} $
Substituting the above value of $ {{\tan }^{2}}\theta $ in the given expression we get,
 $ \begin{align}
  & 2\left( {{\sec }^{2}}\theta +{{\tan }^{2}}\theta \right)-7 \\
 & =2\left( {{\sec }^{2}}\theta +{{\sec }^{2}}\theta -1 \right)-7 \\
 & =4{{\sec }^{2}}\theta -9 \\
\end{align} $
It is given that:
 $ \cos \theta =\dfrac{2}{3} $
As we have converted the given expression in terms of $ \sec \theta $ so we need the value of $ \sec \theta $ . We have given the value of $ \cos \theta $ so from the trigonometry we know that the inverse of $ \cos \theta $ is $ \sec \theta $ . So, taking the reciprocal of $ \cos \theta $ we get,
 $ \sec \theta =\dfrac{3}{2} $
Substituting this value of $ \sec \theta $ in the expression $ 4{{\sec }^{2}}\theta -9 $ we get,
 $ \begin{align}
  & 4{{\left( \dfrac{3}{2} \right)}^{2}}-9 \\
 & =4\left( \dfrac{9}{4} \right)-9 \\
 & =9-9=0 \\
\end{align} $
From the above calculation, the value of the given expression is 0.
Hence, the correct option is (b).

Note: In the above solution instead of using the identity $ 1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta $ we can substitute the value of the tan θ in the given expression 2sec2θ + 2tan2θ – 7. Now, we can find the value of tan θ as follows:
 $ \cos \theta =\dfrac{2}{3} $
In the below diagram, we have shown a triangle ABC right angled at B along with an angle $ \theta $ .

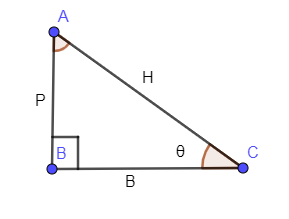
In the above figure, “P” stands for perpendicular with respect to angle θ, “B” stands for the base with respect to angle θ and “H” stands for the hypotenuse with respect to angle θ.

We know that, $ \cos \theta $ is equal to base divided by hypotenuse so using Pythagoras theorem we can find the perpendicular of the triangle.
  $ \cos \theta =\dfrac{B}{H} $
 $ \begin{align}
  & {{H}^{2}}={{B}^{2}}+{{P}^{2}} \\
 & \Rightarrow 9=4+{{P}^{2}} \\
 & \Rightarrow {{P}^{2}}=5 \\
 & \Rightarrow P=\sqrt{5} \\
\end{align} $
From the above calculation, we can find the value of $ \tan \theta $ :
 $ \tan \theta =\dfrac{\sqrt{5}}{2} $
Substituting this value of $ \tan \theta $ in the given expression we get,
\[\begin{align}
  & 2\left( {{\sec }^{2}}\theta +{{\tan }^{2}}\theta \right)-7 \\
 & =2\left( \dfrac{9}{4}+\dfrac{5}{4} \right)-7 \\
 & =2\left( \dfrac{14}{4} \right)-7 \\
 & =7-7=0 \\
\end{align}\]
Hence, we have got the answer as 0.