Question

If $\cos \left( 2{{\sin }^{-1}}x \right)=\dfrac{1}{9}$, then find the value of x.

Answer 1

Hint: Use the fact that $\cos 2x=1-2{{\sin }^{2}}x$ and hence prove that $\cos \left( 2{{\sin }^{-1}}x \right)=1-2{{\sin }^{2}}\left( {{\sin }^{-1}}x \right)$. Use the fact that $\sin \left( {{\sin }^{-1}}x \right)=x\forall x\in \left[ -1,1 \right]$ and hence prove that the given equation is equivalent to the equation $1-2{{x}^{2}}=\dfrac{1}{9}$ in the interval $\left[ -1,1 \right]$. Hence find the value of x in the given interval which satisfies the given equation. Verify your answer.

Complete step-by-step answer:

Before dwelling into the solution of the above question, we must understand how ${{\sin }^{-1}}x$ is defined even when $\sin x$ is not one-one.
We know that sinx is a periodic function.
Let us draw the graph of sinx

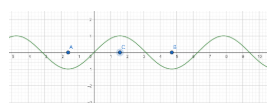
As is evident from the graph sinx is a repeated chunk of the graph of sinx within the interval $\left[ A,B \right]$ , and it attains all its possible values in the interval $\left[ A,C \right]$. Here $A=\dfrac{-\pi }{2},B=\dfrac{3\pi }{2}$ and $C=\dfrac{\pi }{2}$
Hence if we consider sinx in the interval [A, C], we will lose no value attained by sinx, and at the same time, sinx will be one-one and onto.
Hence $\arcsin x$ is defined over the domain $\left[ -1,1 \right]$, with codomain $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]$ as in the domain $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]$, sinx is one-one and ${{R}_{\sin x}}=\left[ -1,1 \right]$.
Now, we have $y={{\sin }^{-1}}x\Rightarrow x=\sin y$
Hence, we have $\sin \left( {{\sin }^{-1}}x \right)=\sin y=x$ provided x in the domain $\left[ -1,1 \right]$.
Now, we know that $\cos 2x=1-2{{\sin }^{2}}x$
Replace x by ${{\sin }^{-1}}x$, we get
$\cos \left( 2{{\sin }^{-1}}x \right)=\grave{\ }1-2{{\sin }^{2}}\left( {{\sin }^{-1}}x \right)$
Now, we know that $\sin \left( {{\sin }^{-1}}x \right)=x$
Hence ,we have $\cos \left( 2{{\sin }^{-1}}x \right)=1-2{{x}^{2}},x\in \left[ -1,1 \right]$
Hence, we have $1-2{{x}^{2}}=\dfrac{1}{9}$
Adding $2{{x}^{2}}$ on both sides, we get
$2{{x}^{2}}+\dfrac{1}{9}=1$
Subtracting $\dfrac{1}{9}$ on both sides, we get
$2{{x}^{2}}=\dfrac{8}{9}$
Dividing both sides by 2, we get
${{x}^{2}}=\dfrac{4}{9}\Rightarrow x=\pm \dfrac{2}{3}$
Since both $\dfrac{2}{3}$ and $-\dfrac{2}{3}$ are in the range $\left[ -1,1 \right]$, we have
$x=\dfrac{2}{3}$ and $x=-\dfrac{2}{3}$ are the roots of the given equation.

Note: [1] Verification:
We have x = $\dfrac{2}{3}$
Hence, we have $\cos \left( 2{{\sin }^{-1}}x \right)=1-2{{\left( x \right)}^{2}}=1-2\left( \dfrac{4}{9} \right)=\dfrac{1}{9}$
Similar for $x=-\dfrac{2}{3}$, we have $\cos \left( 2{{\sin }^{-1}}x \right)=\dfrac{1}{9}$.
Hence our answer is verified to be correct.

[2] Graphical method:

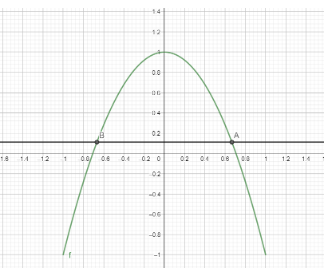
As is evident from the graph two solutions A and B exist.