Question

If \[\cos \alpha = \dfrac{1}{2}\left( {x + \dfrac{1}{x}} \right)\] and \[\cos \beta = \dfrac{1}{2}\left( {y + \dfrac{1}{y}} \right)\]. Evaluate\[\cos \left( {\alpha - \beta } \right)\].

Answer 1

Hint: We know formula for \[\cos \left( {\alpha - \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \].But we have values of cos function only. So we need to find values of sin function using given data and trigonometric functions.

Complete step-by-step answer:
Given that,
\[
  \cos \alpha = \dfrac{1}{2}\left( {x + \dfrac{1}{x}} \right) \\
   \Rightarrow \cos \alpha = \left( {\dfrac{{{x^2} + 1}}{{2x}}} \right) \\
  \cos \beta = \dfrac{1}{2}\left( {y + \dfrac{1}{y}} \right) \\
   \Rightarrow \cos \beta = \left( {\dfrac{{{y^2} + 1}}{{2y}}} \right) \\
\]

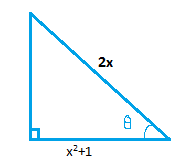
In figure alongside if \[\theta \] is the angle then cos of that angle will be the ratio of adjacent side to hypotenuse. Using that and the theorem of Pythagoras we will find sin function.
According to theorem of Pythagoras,
\[
  hyp{t^2} = bas{e^2} + heigh{t^2} \\
  height = \sqrt {hyp{t^2} - bas{e^2}} \\
   \Rightarrow \sqrt {{{\left( {2x} \right)}^2} - {{\left( {{x^2} + 1} \right)}^2}} \\
   \Rightarrow \sqrt {4{x^2} - \left( {{x^4} + 2{x^2} + 1} \right)} \\
   \Rightarrow \sqrt {4{x^2} - {x^4} - 2{x^2} - 1} \\
   \Rightarrow \sqrt { - {x^4} + 2{x^2} - 1} \\
   \Rightarrow \sqrt { - \left( {{x^4} - 2{x^2} + 1} \right)} \\
   \Rightarrow \sqrt {{i^2}{{\left( {{x^2} - 1} \right)}^2}} \\
   \Rightarrow \left( {{x^2} - 1} \right)i \\
\]
This is the value of the side opposite to the angle that is the height of the triangle.
Now sin function is the ratio of opposite sides to hypotenuses. So sin function is given by
\[\dfrac{{\left( {{x^2} - 1} \right)i}}{{2x}}\]
Now for respective angles just replace the variables.
 \[\cos \left( {\alpha - \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \]
Putting the values,
\[
   \Rightarrow \left( {\dfrac{{{x^2} + 1}}{{2x}}} \right)\left( {\dfrac{{{y^2} + 1}}{{2y}}} \right) + \left( {\dfrac{{\left( {{x^2} - 1} \right)i}}{{2x}}} \right)\left( {\dfrac{{\left( {{y^2} - 1} \right)i}}{{2y}}} \right) \\
   \Rightarrow \dfrac{{\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right)}}{{4xy}} + \dfrac{{\left( {\left( {{x^2} - 1} \right)i} \right)\left( {\left( {{y^2} - 1} \right)i} \right)}}{{4xy}} \\
\]
Multiplying the brackets separately,
\[ \Rightarrow \dfrac{{{x^2}{y^2} + {x^2} + {y^2} + 1}}{{4xy}} + \dfrac{{({x^2}{y^2} - {x^2} - {y^2} + 1){i^2}}}{{4xy}}\]
Putting the value of \[{i^2}\]=-1
\[ \Rightarrow \dfrac{{{x^2}{y^2} + {x^2} + {y^2} + 1}}{{4xy}} - \dfrac{{({x^2}{y^2} - {x^2} - {y^2} + 1)}}{{4xy}}\]
Multiplying the second term with minus sign,
\[ \Rightarrow \dfrac{{{x^2}{y^2} + {x^2} + {y^2} + 1 - {x^2}{y^2} + {x^2} + {y^2} - 1}}{{4xy}}\]
Cancelling the opposite sign terms and rewriting the equation,
\[
   \Rightarrow \dfrac{{2({x^2} + {y^2})}}{{4xy}} \\
   \Rightarrow \dfrac{1}{2}\left( {\dfrac{{{x^2}}}{{xy}} + \dfrac{{{y^2}}}{{xy}}} \right) \\
   \Rightarrow \dfrac{1}{2}\left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) \\
\]
This is the final value of \[\cos \left( {\alpha - \beta } \right)\].

Note: Using any other trigonometric identity student might get the answer but that will be tedious so use Pythagoras theorem for convenience. Always pay attention towards the signs of terms. Go step by step because skipping a single step might confuse a student.