Question

If corresponding angles of two triangles are equal, then they are known as
A.Equiangular triangles
B.Adjacent angles
C.Supplementary angles
D.Complementary angles

Answer 1

Hint: In this question we are given that there are two triangles whose corresponding angles are equal then what we called them. We have given four options by analysing each option we can give the answer.
If the sum of two angles is equal to ${180^ \circ }$then they are supplementary angles and if the sum of two angles is equal to ${90^ \circ }$ then they are called complementary angles. By defining all the options, we can see which option matches with corresponding angles of the two triangles.

Complete step-by-step answer:
First of all, let us see what is given to us? We have given two triangles whose corresponding angles are equal.
We have to tell what these types of triangles are called. We have four options and discuss each option one by one as follows,
Option A: Equiangular triangle
let us take two triangles i.e. $\vartriangle ABC$ and $\vartriangle PQR$as given below

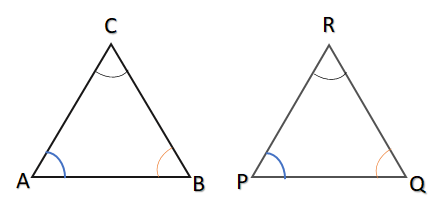
Here in $\vartriangle ABC$ and $\vartriangle PQR$, $\angle A = \angle P,\angle B = \angle Q\& \angle C = \angle R$. Therefore, they made AAA and they didn’t satisfy the congruence property. So, we cannot call them congruent triangles. But their corresponding angles are equal and we can say them as equiangular triangles.
Option B: Adjacent angles
Two angles are said to be adjacent if they have common vertex and one common arm shown below:

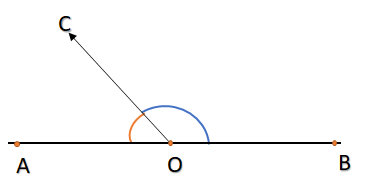
Here, $\angle AOC$ and $\angle BOC$ are adjacent as they have one common vertex O and one common arm CO. As they are the angle between only two lines. Hence, they are not corresponding angles of the triangles.
Option C: Supplementary angles
The angles whose sum is equal to ${180^ \circ }$ then the angles are called supplementary angles as shown below:

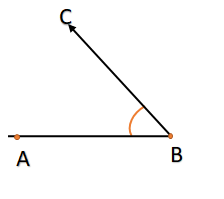
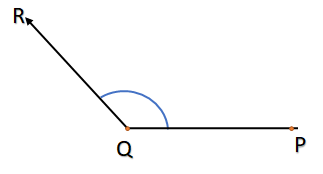
$ \Rightarrow \angle ABC + \angle PQR = {180^ \circ }$
As the sum of angles of a triangle is ${180^ \circ }$. Therefore, these angles are not of triangles.
Option D: complementary angles
The angles whose sum is equal to ${90^ \circ }$ then the angles are called complementary angles as shown below:

$ \Rightarrow \angle ABC + \angle PQR = {90^ \circ }$
As the sum of angles of a triangle is ${90^ \circ }$. These are two angles of between different rays hence can’t be angles of triangle.
By analysing all the options, we conclude that if two triangles have three equal corresponding angles then they are said to be equiangular triangles.
Hence option A is correct

Note: Let’s suppose they have given one more option i.e. congruent triangle then some student tick the option of congruent triangle. This option is wrong because it will form AAA and it doesn’t mean that they are congruent triangles. Four theorems that satisfy congruence property are SSS, SAS, ASA, RHS. If two triangles have these corresponding parameters are equal then they are congruent.
The sum of angles of a triangle are ${180^ \circ }$. No two angles form triangles and hence, we directly cancel the option B, C and D. we left with only option A.