Question

If ${\mathrm{tan\mathrm\theta}}_1{\mathrm{tan\mathrm\theta}}_2=-\dfrac{\mathrm a^2}{\mathrm b^2}$, then the chord joining two points ${\mathrm\theta}_1\;\mathrm{and}\;{\mathrm\theta}_2$ on the ellipse $\dfrac{\mathrm x^2}{\mathrm a^2}+\dfrac{\mathrm y^2}{\mathrm b^2}=1$ will subtend a right angle at-
a)Focus
b)Centre
c)End of major axis
d)End of minor axis

Answer 1

Hint: To solve this problem, one should have knowledge about the parametric form of an ellipse. The parametric form of a general ellipse at point $\mathrm\theta$ is given by-
$\left(\mathrm{acos\mathrm\theta},\;\mathrm{bsin\mathrm\theta}\right)$
The focus is the point about which a conic section is constructed. An ellipse has two foci. The centre is the geometrical centre inside the ellipse. The end of the major axis is the end point of the longer diameter of the ellipse. The end of the minor axis is the end point of the shorter diameter.

Complete step-by-step answer:

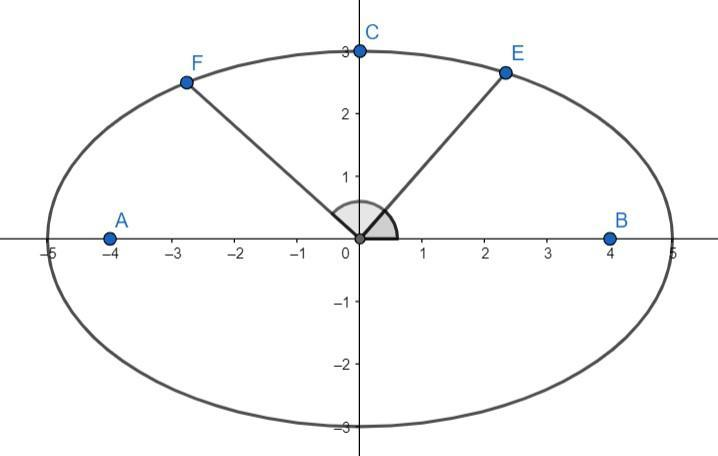
This is the ellipse with equation $\dfrac{\mathrm x^2}{\mathrm a^2}+\dfrac{\mathrm y^2}{\mathrm b^2}=1$. Let the point E and F be at an angle ${\mathrm\theta}_1\;\mathrm{and}\;{\mathrm\theta}_2$ respectively.
By parametric form of ellipse, the coordinates of point E and F are-
$\mathrm E\left({\mathrm{acos\mathrm\theta}}_1,\;{\mathrm{bsin\mathrm\theta}}_1\right)\\\mathrm F\left({\mathrm{acos\mathrm\theta}}_2,\;{\mathrm{bsin\mathrm\theta}}_2\right)$
The slope of a point(p,q) with respect to origin is given by-
$\mathrm m=\dfrac{\mathrm q-0}{\mathrm p-0}=\dfrac{\mathrm q}{\mathrm p}$
So, the slopes of points E and F with respect to origin are-
${\mathrm m}_{\mathrm E}=\dfrac{{\mathrm{bsin\mathrm\theta}}_1}{{\mathrm{acos\mathrm\theta}}_1}=\dfrac{\mathrm b}{\mathrm a}{\mathrm{tan\mathrm\theta}}_1\\{\mathrm m}_{\mathrm F}=\dfrac{{\mathrm{bsin\mathrm\theta}}_2}{{\mathrm{acos\mathrm\theta}}_2}=\dfrac{\mathrm b}{\mathrm a}{\mathrm{tan\mathrm\theta}}_2$
If we multiply $m_E$ and $m_F$, the result should be-
${\mathrm m}_{\mathrm E}\times{\mathrm m}_{\mathrm F}=\dfrac{\mathrm b}{\mathrm a}{\mathrm{tan\mathrm\theta}}_1\times\dfrac{\mathrm b}{\mathrm a}{\mathrm{tan\mathrm\theta}}_2\\=\dfrac{\mathrm b^2}{\mathrm a^2}{\mathrm{tan\mathrm\theta}}_1{\mathrm{tan\mathrm\theta}}_2$
It is given in the question that ${\mathrm{tan\mathrm\theta}}_1{\mathrm{tan\mathrm\theta}}_2=-\dfrac{\mathrm a^2}{\mathrm b^2}$, on substituting the value-
$m_E\times m_F=\dfrac{b^2}{a^2}\times-\dfrac{a^2}{b^2}=-1$
If the product of slopes of two lines is -1, then the lines are perpendicular to each other. Hence, the two points E and F subtend a right angle at the centre of the ellipse.
The correct option is B. Centre

Note: To solve this problem, one should have knowledge about an ellipse as well as the slope of a line. The parametric form of a conic is very useful in solving problems as it reduces the number of variables and the calculation. If it is required to prove two lines to be perpendicular it is sufficient to prove the product of their slopes to be -1.