Question

If ball is thrown vertically upwards with speed u, the distance covered during the last t seconds of its ascent is:
(Take g=10 $m/{s^2}$)
A. $ut$
B. $\dfrac{1}{2}g{t^2}$
C.$ut - \dfrac{1}{2}g{t^2}$
D. $(u + gt)t$

Answer 1

Hint: In order to solve this above question, draw a diagram by considering the ball which is thrown upwards, then using the equation of motion and the time of ascent we can find out the distance covered in the last second.

Complete step by step answer:
Let us take the total height to be taken as H.
Time of ascent can be taken as T.

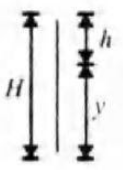
From the second equation of motion,
So, H=$ut - \dfrac{1}{2}g{t^2}$……. (1)
Distance covered by ball in time (T - t) sec.
Substitute the value in equation (1) by taking H=y
$y=u (T−t)-\dfrac{1}{2}g{(T - t)^2}$
From the diagram, the distance covered by the ball in last t sec.
h=H−y
$\Rightarrow h=ut - \dfrac{1}{2}g{t^2} - u (T−t) -\dfrac{1}{2}g{(T - t)^2}$
By solving and putting time of ascent T=$\dfrac{u}{g}$ we will get
$\therefore h=\dfrac{1}{2}g{t^2}$
Hence the correct option is B.

Note: If the ball reaches to the topmost position then velocity of ball is taken as zero. Then we can find the distance covered in last t sec by applying the same method for the time of descent. The total time taken by the ball is called the time of flight. The time of flight of projectile motion is defined as the time from when the object is projected to the time it reaches the surface.