Question

If ${{b}^{2}}-4ac=0$ then the graph of $y=a{{x}^{2}}+bx+c$
(a) Cuts x – axis in two real points.
(b) Touches x – axis.
(c) Lies entirely above the x – axis.
(d) Cannot be determined.

Answer 1

Hint: Here we will understand the three different cases related to the values of the discriminant of a quadratic equation. They are D < 0, D > 0 and in the end D = 0, where D is called the discriminant given as $D={{b}^{2}}-4ac$. Further, we will see the nature of the graph in the three cases and the number of solutions they have.

Complete step-by-step solution:
Here we have been provided with the function $y=a{{x}^{2}}+bx+c$ and we are asked to find the nature of the graph of this curve if we have the condition ${{b}^{2}}-4ac=0$. Let us check all the cases related to the value of the discriminant one by one.
We know that the solution of a quadratic equation $a{{x}^{2}}+bx+c=0$ is given by the discriminant formula as $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$. Here ${{b}^{2}}-4ac=D$ where D denotes the discriminant value. Now three cases arise for the value of D, let us check them one by one.
(1) When we have D < 0, i.e. ${{b}^{2}}-4ac<0$.
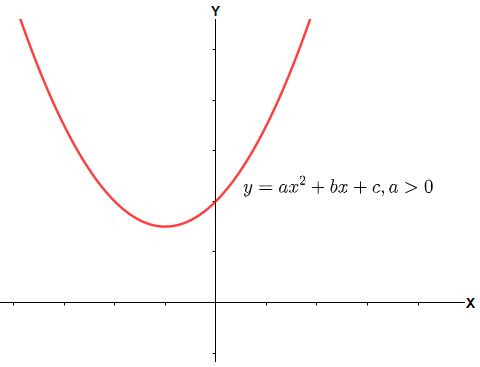
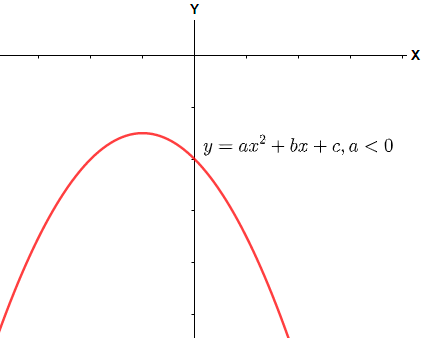
Now, in such a case we have the term inside the square root sign negative that means we have two complex roots of the equation and that cannot be represented on a real plane. Therefore the curve will lie either entirely above the x – axis (for a > 0) or entirely below the x – axis (for a < 0). The graphs can be shown as below.
Graph for a > 0.

Graph for a < 0.

(2) When we have D > 0, i.e. ${{b}^{2}}-4ac>0$.
Now, in such a case we have two different roots of the quadratic equation because one time we have to consider positive sign and the other time the negative sign in the solution $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$. Therefore, the graph of the equation will cut the cut x – axis at two different places which can be shown below.

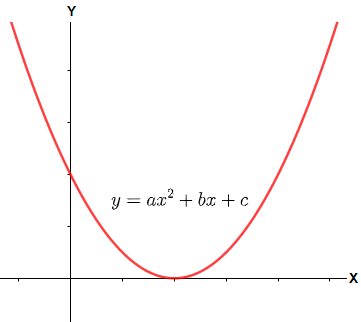
(3) When we have D = 0, i.e. ${{b}^{2}}-4ac=0$.
Now, in such a case we have only one root of the quadratic equation and that will be $x=\dfrac{-b}{2a}$. Therefore, the graph of the equation will cut the cut x – axis at one point, in other words it will touch the x – axis, which can be shown below.

Hence, option (b) is the correct answer.

Note: Note that the nature of the concavity of the parabola depends completely on the value of ‘a’. In case ‘a’ is less than 0 then parabola opens downwards and in case ‘a’ is greater than 0 then parabola opens upward. There is another type of parabola given as $x=a{{y}^{2}}+by+c$ that opens sideways (either leftward or rightward). You must remember all the cases that we have discussed above.