Question

If b > a, then prove that the length of the tangent drawn from any point on circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+a=0$ to the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+b=0$ is $\sqrt{b-a}$.

Answer 1

Hint: For solving this problem, we first show the condition of the length of tangent using a diagram. Also, the relation between tangent and equation of a circle at a point is important. Then by using this property, we can prove the desired result.

Complete step by step answer:
According to the question, we are given two equations of a circle. So, let the inner circle with constant as a be equation (1) and outer circle with constant b be (2):
$\begin{align}
  & {{x}^{2}}+{{y}^{2}}+2gx+2fy+a=0\ldots (1) \\
 & {{x}^{2}}+{{y}^{2}}+2gx+2fy+b=0\ldots (2) \\
\end{align}$
Now, the length of the tangent can be shown by using the diagram as:

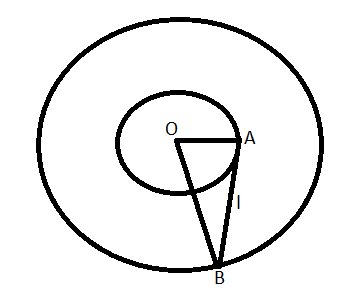
Also, we know that length of tangent to any circle at a point is equal to the square root value of the circle at that point. This can be mathematically expressed as:
For a circle with equation ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$, the length of tangent at (l, m) would be:
$Length=\sqrt{{{l}^{2}}+{{m}^{2}}+2gl+2fm+c}$
Consider a point $\left( {{x}_{1}},{{y}_{1}} \right)$ on the inner circle such that it satisfies the circle equation. Therefore, we form equation (3) as:
$\begin{align}
  & {{x}_{1}}^{2}+{{y}_{1}}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+a=0 \\
 & \therefore {{x}_{1}}^{2}+{{y}_{1}}^{2}+2g{{x}_{1}}+2f{{y}_{1}}=-a\ldots (3) \\
\end{align}$
Now, the length of tangent from point $\left( {{x}_{1}},{{y}_{1}} \right)$ to outer circle would be:
$l=\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+b}\ldots (4)$
Putting the values from equation (3) into (4), we get
$l=\sqrt{b-a}$
Since the left-hand side and right-hand side of the equation are equal, we proved the equivalence of both sides. So, we obtain the desired result.

Note: The key concept for solving this problem is the knowledge of length of tangent at a point on any circle. It is a very important property of geometry and is very helpful in solving complex problems without dealing with much calculation. So, the length of tangent is obtained easily