Question

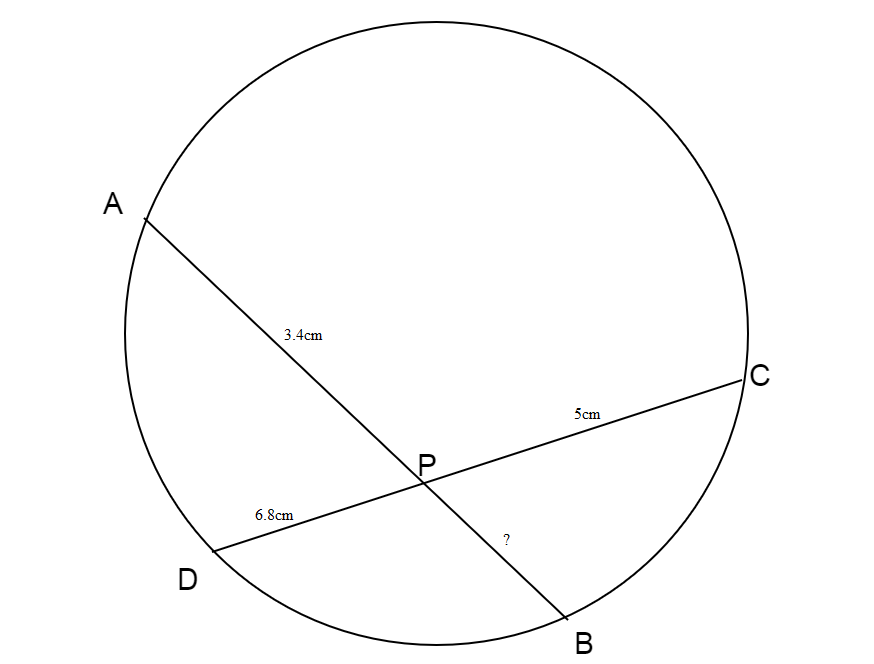
If AP = 3.4cm, CP = 5cm and DP = 6.8cm, then PB is equal to
A. \[8\] cm
B. \[9\] cm
C. \[10\] cm
D. \[12\] cm

Answer 1

Hint:
Here we use the property of intersection of two chords which gives us formula for lengths of line segments formed by intersection of two chords i.e. If two chords in a circle intersect at a point, then the product of length of line segments of one chord is equal to the product of length of line segments of other chord.
* In a circle chord is a line joining two points lying on the circumference of the circle. Therefore chords may/may not have different lengths.

Complete step by step solution:
Given, \[AB\]and \[CD\]are two chords which intersect at point \[P\] gives us four line segments \[AP,PB,CP,DP\].
Also, \[AB = AP + PB,CD = CP + PD\]
Therefore, intersection at point \[P\] gives
\[AP = 3.4cm,{\text{ }}CP = 5cm{\text{ ,}}DP = 6.8cm\] From the property of intersection of chords, If two chords in a circle intersect at a point, then the product of length of line segments of one chord is equal to the product of length of line segments of other chord.
Therefore, lengths \[AP \times PB = CP \times PD\].
Substitute value of lengths of line segments AP=3.4cm, CP=5cm and DP=6.8cm in equation \[AP \cdot PB = CP \cdot PD\]
\[3.4 \times PB = 5 \times 6.8\]
Divide both sides of the equation by 3.4
\[\dfrac{{3.4 \times PB}}{{3.4}} = \dfrac{{5 \times 6.8}}{{3.4}}\]

Factor out the common factors from both sides.
\[PB = 5 \times 2\]
Perform multiplication to obtain the length of PB.
\[PB = 10\,\,cm\]

Therefore, PB=10cm. So,Option C is correct.

Note:
Similar situation may arise when the chords intersect outside the circle. The approach to these would be the same. Using the product of line segments of chords lengths of unknown segments can be obtained irrespective of where the chords intersect.
* In a circle, diameter is the longest chord that can be drawn from one point on the circumference to another point. Also, diameter is twice the length of the radius.