Question

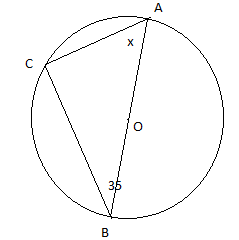
If \[AOB\] is the diameter of the circle and \[\angle B = {35^ \circ }\], then find the value of \[x.\]

Answer 1

Hint: We know that the angle subtended by a diameter of semicircle on any point of circle is \[{90^ \circ }\].
We know that the sum of all the angles of a triangle is \[{180^ \circ }\]. This property is known as angle sum property.
Using these two theorems we can find the value of the third angle.

Complete step-by-step solution:
It is given that; \[AOB\] is the diameter of the circle and \[\angle B = {35^ \circ }\].
We have to find the value of \[x\]
We know that the angle subtended by a diameter or semi-circle on any point of circle is \[{90^ \circ }\].
In the triangle, \[ABC\], it is given that, \[AOB\] is the diameter of the circle. So, the angle subtended (The angle made by something from a given viewpoint is known as subtended angle) by a diameter is \[\angle ACB\].
So, \[\angle ACB = {90^ \circ }\]
So, in the triangle, \[ABC\]
\[\angle ACB = {90^ \circ }\] and \[\angle ABC = {35^ \circ }\]
Again, we know that, the sum of all the angles of triangle is \[{180^ \circ }\]
Therefore, we have,
\[\angle ACB + \angle ABC + \angle BAC = {180^ \circ }\]
Substitute the values we get,
\[{90^ \circ } + {35^ \circ } + x = {180^ \circ }\]
Simplifying we get,
\[x = {55^ \circ }\]

Hence, the value of \[x\] is \[{55^ \circ }\]

Note: We have in mind that Thales theorem states that any diameter of a circle subtends a right angle to any point on the circle. This is a particular case of Thales theorem, which applies to an entire circle, not just a semicircle. Angle sum property of triangle states that the sum of interior angles of a triangle is ${180^ \circ }$