Question

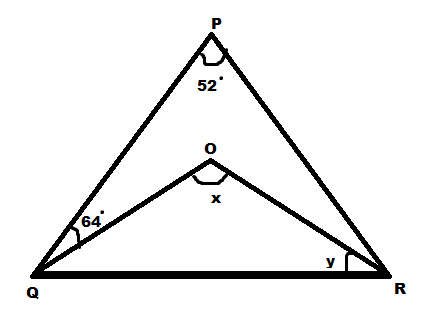
If $\angle P = {52^ \circ }$ and $\angle PQO = {64^ \circ }$ . If QO and RO are bisectors of $\angle PQR{\text{ and }}\angle PRQ$ respectively, then the value of $\angle x$ exists but the value of $\angle y$ does not exist?
a.True
b.False

Answer 1

Hint: We are given that OQ and OR are angle bisectors from which we get $\angle PQO = \angle OQR$ and $\angle PRO = \angle ORQ$ and by using the angle sum property of a triangle we can find that y does not exist and using the same property in the triangle OQR we can see that the value of x exists as the value of y does not exist.

Complete step-by-step answer:

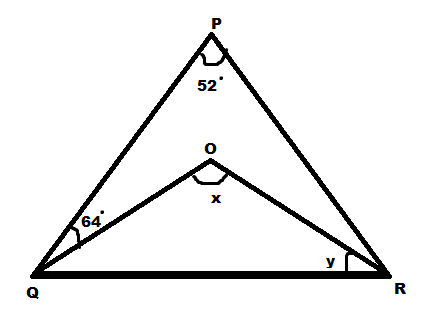
We are given that OQ is the angle bisector of $\angle PQR$
From that we have $\angle PQO = \angle OQR$
We are given that $\angle PQO = {64^ \circ }$
Hence $\angle OQR = {64^ \circ }$
We are given that OR is the angle bisector of $\angle PRQ$
From that we have $\angle PRO = \angle ORQ$
We are given that $\angle ORQ = y$
Hence $\angle PRO = y$
We know that the sum of the angles of a triangle is equal to ${180^ \circ }$
\[
   \Rightarrow \angle P + \angle Q + \angle R = {180^ \circ } \\
   \Rightarrow {52^ \circ } + (\angle PQO + \angle OQR) + (\angle PRO + \angle ORQ) = {180^ \circ } \\
   \Rightarrow {52^ \circ } + ({64^ \circ } + {64^ \circ }) + (y + y) = {180^ \circ } \\
   \Rightarrow {180^ \circ } + 2y = {180^ \circ } \\
   \Rightarrow 2y = {180^ \circ } - {180^ \circ } = 0 \\
\]
Therefore from this we get that y does not exists
Now in triangle OQR ,
\[
   \Rightarrow \angle QOR + \angle OQR + \angle ORQ = {180^ \circ } \\
   \Rightarrow x + {64^ \circ } + y = {180^ \circ } \\
   \Rightarrow x + y = {180^ \circ } - {64^ \circ } \\
   \Rightarrow x + y = {116^ \circ } \\
    \\
\]
Therefore here we get that the value of x exists only when the value of y does not exist.
Therefore the statement is true.
The correct option is a.

Note: An acute triangle is one in which each of the three angles is acute – less than 90 degrees. A right triangle is one in which it has one right angle – 90degrees. An obtuse triangle is defined as a triangle that has one obtuse angle – more than 90 degrees.