Question

If $\angle B$ and $\angle Q$ are acute angles such that sinB = sinQ then prove that $\angle B=\angle Q$

Answer 1

Hint: First we will draw the given diagram of two triangles ABC and PQR. It is given that angle B and Q are acute, we will use the general formula of sin and then substitute the given values in that formula. We will show that $\angle B=\angle Q$ is true.

Complete step-by-step answer:

Let’s draw the required diagram first.

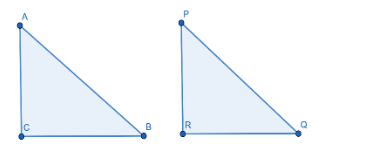
Now we have been given that $\angle B$ and $\angle Q$ are acute angles.
And it is also given that sinB = sinQ
Now we will use the formula for general solution of sin,
Now, if we have $\sin \theta =\sin \alpha $ then the general solution is:
$\theta =n\pi +{{\left( -1 \right)}^{n}}\alpha $
Now using the above formula for sinB = sinQ we get,
$B=n\pi +{{\left( -1 \right)}^{n}}Q$, where n = integers.
Now as it is given that $\angle B$ and $\angle Q$ are acute angles, so for B to be acute the value of n must be 0.
Hence, substituting the value of n =0 in $B=n\pi +{{\left( -1 \right)}^{n}}Q$ we get,
$\begin{align}
  & B=0\pi +{{\left( -1 \right)}^{0}}Q \\
 & B=Q \\
\end{align}$
Hence, we have proved that $\angle B=\angle Q$, if $\angle B$ and $\angle Q$ are acute angles.

Note: The formula for general solution of sin must be kept in mind. Student must note that how we have used the given information that $\angle B$ and $\angle Q$ are acute angles, with that information we have reduced the possibility of infinite solution to only solution in the equation $B=n\pi +{{\left( -1 \right)}^{n}}Q$. Hence, these methods are very important.