Question

If $a\ne 0$ and the line \[2bx+3cy+4d=0\] passes through the points of intersection of the parabola \[{{y}^{2}}=4ax\] and \[{{x}^{2}}=4ay\], prove that \[{{d}^{2}}+{{\left( 2b+3c \right)}^{2}}=0\].

Answer 1

Hint: We have to find the values of \[x\] and \[y\] to get the points of intersection of the two parabolas by rearranging the two equations \[{{y}^{2}}=4ax\] and \[{{x}^{2}}=4ay\]. Then, it can be substituted in the equation of the line.

Complete step-by-step answer:
Two parabolas \[{{y}^{2}}=4ax\] and \[{{x}^{2}}=4ay\] are given in the question. A line that passes through the points of their intersection is given as $2bx+3cy+4d=0$. Let us consider the plot as below,

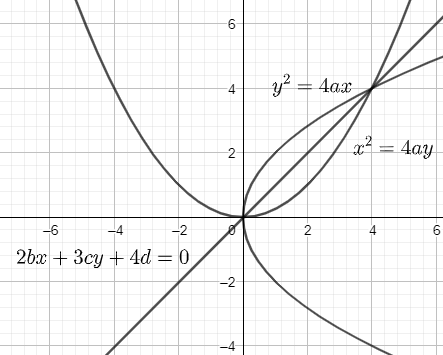
The first step is to find the points of intersection of the parabolas. Let us consider the two equations as below,
\[{{y}^{2}}=4ax\ldots \ldots \ldots \left( i \right)\]
\[{{x}^{2}}=4ay\ldots \ldots \ldots \left( ii \right)\]
From equation \[\left( ii \right)\], we can substitute $y=\dfrac{{{x}^{2}}}{4a}$ in equation $\left( i \right)$. Therefore, we get
$\begin{align}
  & {{\left[ \dfrac{{{x}^{2}}}{4a} \right]}^{2}}=4ax \\
 & \dfrac{{{x}^{4}}}{16{{a}^{2}}}=4ax \\
 & \dfrac{{{x}^{4}}}{16{{a}^{2}}}-4ax=0 \\
\end{align}$
Taking LCM, we get,
\[\begin{align}
  & \dfrac{{{x}^{4}}-64{{a}^{3}}x}{16{{a}^{2}}}=0 \\
 & {{x}^{4}}-64{{a}^{3}}x=0 \\
\end{align}\]
Taking the common term \[x\] outside, we get
\[x\left( {{x}^{3}}-64{{a}^{3}} \right)=0\]
We can have the values of \[x\] as,
\[x=0\] and
\[\begin{align}
  & {{x}^{3}}-64{{a}^{3}}=0 \\
 & {{x}^{3}}=64{{a}^{3}} \\
\end{align}\]
Taking the cube root, we get
\[x=4a\]
Therefore, the values of \[x\] are \[0\] and $4a$.
Substituting the value of \[x=0\] in equation $\left( i \right)$, we can find the value of \[y\] as,
$\begin{align}
  & {{y}^{2}}=4a\times 0 \\
 & y=0 \\
\end{align}$
Substituting the value of \[x=4a\] in equation $\left( i \right)$, we can find the value of \[y\] as,
$\begin{align}
  & {{y}^{2}}=4a\times 4a \\
 & y=4a \\
\end{align}$
Therefore, the values of \[y\] are also obtained as \[0\] and $4a$.
So, the points of intersection of the parabolas \[{{y}^{2}}=4ax\] and \[{{x}^{2}}=4ay\] are \[\left( 0,0 \right)\] and \[\left( 4a,4a \right)\].
Now, since it is given that the line \[2bx+3cy+4d=0\] passes through the intersection points of the parabolas, we can substitute each of these points in the equation of the line.
Substituting point \[\left( 0,0 \right)\] first, we get
\[\begin{align}
  & 2b\times 0+3c\times 0+4d=0 \\
 & d=0 \\
\end{align}\]
Next, substituting point \[\left( 4a,4a \right)\], we get
\[\begin{align}
  & 2b\times 4a+3c\times 4a+4d=0 \\
 & 8ba+12ca+4d=0 \\
\end{align}\]
Since we have the result \[d=0\], we get,
$8ba+12ca=0$
Taking out the common term $4a$, we get
\[\begin{align}
  & 4a\left( 2b+3c \right)=0 \\
 & 2b+3c=0 \\
 & 2b=-3c \\
\end{align}\]
As per the question, we have to prove that \[{{d}^{2}}+{{\left( 2b+3c \right)}^{2}}=0\].
The value of \[d\] is \[0\] and also we have $2b=-3c$. Considering the \[LHS\] of the expression to be proved,
\[\begin{align}
  & {{d}^{2}}+{{\left( 2b+3c \right)}^{2}} \\
 & {{0}^{2}}+{{\left( 2b-2b \right)}^{2}} \\
 & 0+0 \\
 & 0=RHS \\
\end{align}\]
Since \[LHS\] is equal to \[RHS\], it is proved.

Note: The points of intersection of two parabolas can be found by looking at the equations given in the question, i.e. \[{{y}^{2}}=4ax\] and \[{{x}^{2}}=4ay\]. When we substitute \[x=0\] in both equations, we get\[y=0\]. Also, the term $4a$ is common to both and the equations have a square term on the \[LHS\]. So, that is possible only when we have \[x=y=4a\].