Question

If an object is held at a distance of \[60\,cm\] from a convex mirror of focal length \[20\,cm\] . What distance from the convex mirror, should a plane mirror be held so that images in the two mirrors coincide?

Answer 1

Hint:For a convex mirror, the sign conventions must be accurate as the distance from the mirror towards the left is taken as negative and the focus is positive. The distance from the object to the image is found when you take the appropriate summation.

Formula used:
The value of focal length of a convex mirror is given by:
\[\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}\]

Complete step by step answer:

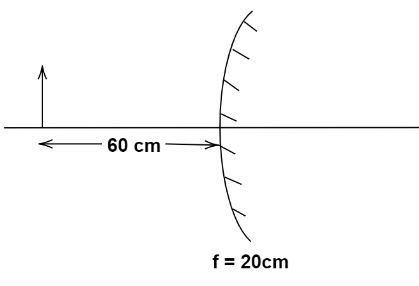
The following data is given in the solution:
The focal length of the convex mirror, \[f = 20\,cm\].
The distance between the object and the convex mirror, \[u = 60\,cm\].
From the formula \[\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}\]
We find the value of \[v = \dfrac{{uf}}{{u - f}}\]
But since our mirror is a convex mirror and the sign convention tells us that the value of \[u\] will be negative, hence we have,
\[v = \dfrac{{ - 60 \times 20}}{{ - 60 - 20}} \\
\Rightarrow v = \dfrac{{ - 1200}}{{ - 80}} \\
\Rightarrow v = 15\,cm\]

This distance is the separation between the mirror and the image, so the separation or the distance between the image and the object would be the sum of the distance from the object to the mirror and the distance between the image and the mirror.Therefore, the distance between the object and the image will be: \[60 + 15 = 75cm\]

The plane mirror should be placed In between this separation of the image and the object in order for the images to coincide. Hence the plane mirror should be placed at
\[\dfrac{{75}}{2} = 37.5\,cm\]
Now to find the distance of the plane mirror from the concave mirror, we subtract the distance from the object to the convex mirror and the distance from the object to the plane mirror.
\[60\,cm - 37.5\,cm = 22.5\,cm\]

Therefore, the plane mirror must be kept at a distance of \[22.5\,cm\] to the left from the convex mirror.

Note:For a convex mirror, the sign conventions must be accurate as the distance from the mirror towards the left is taken as negative and the focus is positive. The sign convention for this kind of mirror can be very confusing. We use the cartesian sign convention system for easier and better calculation.