Question

If $A\left( -5,7 \right),B\left( -4,5 \right),C\left( -1,6 \right)$ and $D\left( 4,5 \right)$ are the vertices of a quadrilateral, then find its area.

Answer 1

Hint: Divide the quadrilateral ABDC into two triangles ABC and BCD. Find the areas of the triangle ABC and BCD and hence find the area of the quadrilateral ABDC.
Use the property that if $A\equiv \left( {{x}_{1}},{{y}_{1}} \right),B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ and $C\equiv \left( {{x}_{3}},{{y}_{3}} \right)$ then the area of the triangle ABC is given by $\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$.

Complete step-by-step answer:

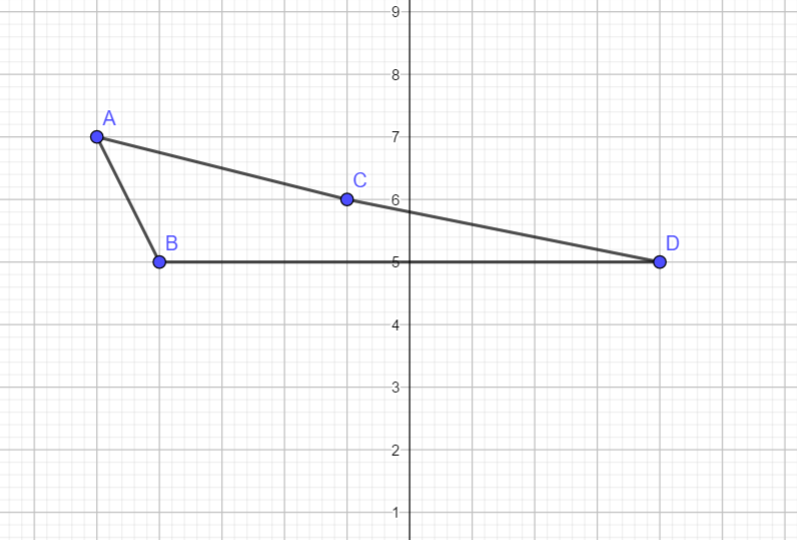
(Note that although ADC appears to be a straight line, it is not actually a straight line. This can be verified by finding the distances AC, CD and AD using distance formula and checking that $AD\ne AC+CD$)
We have by distance formula, $AC=\sqrt{{{\left( -5+4 \right)}^{2}}+{{\left( 7-5 \right)}^{2}}}=\sqrt{1+4}=\sqrt{5}$
Similarly by distance formula, we have $AD=\sqrt{{{\left( -5+1 \right)}^{2}}+{{\left( 7-6 \right)}^{2}}}=\sqrt{16+1}=\sqrt{17}$ and $CD=\sqrt{{{\left( -4+1 \right)}^{2}}+{{\left( 5-6 \right)}^{2}}}=\sqrt{9+1}=\sqrt{10}$. Clearly, we have $AC\ne CD+AD$. Hence, A,C and D are not collinear.
Finding the area of triangle ABC:
We know that if $A\equiv \left( {{x}_{1}},{{y}_{1}} \right),B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ and $C\equiv \left( {{x}_{3}},{{y}_{3}} \right)$ then the area of the triangle ABC is given by $\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$.
We have ${{x}_{1}}=-5,{{x}_{2}}=-4,{{x}_{3}}=-1,{{y}_{1}}=7,{{y}_{2}}=5$ and ${{y}_{3}}=6$
Hence the area of triangle ABC $=\dfrac{1}{2}\left| -5\left( 5-6 \right)-4\left( 6-7 \right)-1\left( 7-5 \right) \right|=\dfrac{1}{2}\left| 5+4-2 \right|=\dfrac{7}{2}=3.5$ square units.
Finding the area of the triangle BCD:
We know that if $A\equiv \left( {{x}_{1}},{{y}_{1}} \right),B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ and $C\equiv \left( {{x}_{3}},{{y}_{3}} \right)$ then the area of the triangle ABC is given by $\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$.
We have ${{x}_{1}}=-4,{{x}_{2}}=-1,{{x}_{3}}=4,{{y}_{1}}=5,{{y}_{2}}=6$ and ${{y}_{3}}=5$
Hence the area of the triangle BCD $=\dfrac{1}{2}\left| -4\left( 6-5 \right)-1\left( 5-5 \right)+4\left( 5-6 \right) \right|=\dfrac{1}{2}\left| -4-0-4 \right|=4$ square units
Hence the area of the quadrilateral ABDC = 4+3.5 = 7.5 square units.

Note: Alternative solution: Best Method.
If $A\equiv \left( {{x}_{1}},{{y}_{1}} \right),B\equiv \left( {{x}_{2}},{{y}_{2}} \right),C\equiv \left( {{x}_{3}},{{y}_{3}} \right)$ and $D\equiv \left( {{x}_{4}},{{y}_{4}} \right)$ are the vertices of a quadrilateral ABCD, then the area of the quadrilateral is given by
$\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}}-{{x}_{3}} & {{y}_{1}}-{{y}_{3}} \\
   {{x}_{2}}-{{x}_{4}} & {{y}_{2}}-{{y}_{4}} \\
\end{matrix} \right|$
Here we have ${{x}_{1}}=-5,{{x}_{2}}=-4,{{x}_{3}}=4,{{x}_{4}}=-1,{{y}_{1}}=7,{{y}_{2}}=5,{{y}_{3}}=5$ and ${{y}_{4}}=6.$
Hence the area of the quadrilateral ABDC is given by $\dfrac{1}{2}\left| \begin{matrix}
   -5-4 & 7-5 \\
   -4+1 & 5-6 \\
\end{matrix} \right|=\dfrac{1}{2}\left| \begin{matrix}
   -9 & 2 \\
   -3 & -1 \\
\end{matrix} \right|=\dfrac{1}{2}\left( 9+6 \right)=\dfrac{15}{2}=7.5$ square units, which is same as obtained above.