Question

If $A\left( 3,2,0 \right),B\left( 5,3,2 \right)\And C\left( -9,6,-3 \right)$ are the vertices of $\Delta ABC$ and the bisector of $\angle BAC$ meets BC at D, then coordinates of D are:
(a) $\left( \dfrac{19}{8},\dfrac{57}{16},\dfrac{17}{16} \right)$
(b) $\left( -\dfrac{19}{8},\dfrac{57}{16},\dfrac{17}{16} \right) $
(c) $\left( \dfrac{19}{8},-\dfrac{57}{16},\dfrac{17}{16} \right)$
(d) None of these

Answer 1

Hint: First of all draw a $\Delta ABC$ and then draw the angle bisector of angle A. The angle bisector of angle A meets BC at point D. Now, the ratio of BD and DC is equal to the ratio of AB and AC. We know the coordinates of A, B and C so using the distance formula we can find the distances AB and AC. The distance formula for two points say $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\And Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$. Substitute the lengths of AB and AC in the ratio equation after substitution you will get the ratio in which point D divides B and C then using the section formula we will find the coordinates of D.

Complete step by step answer:
In the below figure, we have drawn a triangle ABC with an angle bisector of angle A which meets BC at D.
  

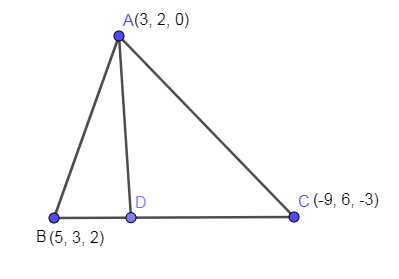
There is a property of angle bisectors that it divides the opposite side in the ratio equal to the ratio of the remaining sides.
$\dfrac{BD}{DC}=\dfrac{AB}{AC}$ ………….Eq. (1)
Now, using the distance formula of the two points we are going to find the distances of AB and AC.
The distance formula between two points say $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\And Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is equal to:
$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$
Using this distance formula, we are going to find the distance between A and B, distance between A and C.
The coordinates of points A and B are $A\left( 3,2,0 \right),B\left( 5,3,2 \right)$ and distance between them is equal to:
$\begin{align}
  & \sqrt{{{\left( 5-3 \right)}^{2}}+{{\left( 3-2 \right)}^{2}}+{{\left( 2-0 \right)}^{2}}} \\
 & =\sqrt{{{\left( 2 \right)}^{2}}+{{\left( 1 \right)}^{2}}+{{\left( 2 \right)}^{2}}} \\
 & =\sqrt{4+1+4} \\
 & =\sqrt{9}=3 \\
\end{align}$
Hence, the length of AB is equal to 3.
The coordinates of A and C are $A\left( 3,2,0 \right),C\left( -9,6,-3 \right)$ and distance between them is equal to:
$\begin{align}
  & \sqrt{{{\left( -9-3 \right)}^{2}}+{{\left( 6-2 \right)}^{2}}+{{\left( -3-0 \right)}^{2}}} \\
 & =\sqrt{{{\left( -12 \right)}^{2}}+{{\left( 4 \right)}^{2}}+{{\left( -3 \right)}^{2}}} \\
 & =\sqrt{144+16+9} \\
 & =\sqrt{169}=13 \\
\end{align}$
Hence, the length of AC is equal to 13.
Now, substituting the values of AB and AC in eq. (1) we get,
$\dfrac{BD}{DC}=\dfrac{3}{13}$
The above equation shows that the point D divides the side BC into the ratio of 3:13 so using section formula we can find the coordinates of point D.
Section formula for point R that divides the two points say $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\And Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ in the ratio of ${{m}_{1}}:{{m}_{2}}$ so the coordinates R is calculated as follows:
$\left( \dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{z}_{2}}+{{m}_{2}}{{z}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right)$
The coordinates of B and C is given as $B\left( 5,3,2 \right)\And C\left( -9,6,-3 \right)$ with a ratio of 3:13 so using the above section formula we can find the coordinates of point D as:
$\begin{align}
  & D\left( \dfrac{3\left( -9 \right)+13\left( 5 \right)}{16},\dfrac{3\left( 6 \right)+13\left( 3 \right)}{16},\dfrac{3\left( -3 \right)+13\left( 2 \right)}{16} \right) \\
 & =D\left( \dfrac{-27+65}{16},\dfrac{18+39}{16},\dfrac{-9+26}{16} \right) \\
 & =D\left( \dfrac{38}{16},\dfrac{57}{16},\dfrac{17}{16} \right) \\
 & =D\left( \dfrac{19}{8},\dfrac{57}{16},\dfrac{17}{16} \right) \\
\end{align}$

So, the correct answer is “Option a”.

Note: The mistake that could happen is in writing the section formula. In the below, we have written the section formula as:
$\left( \dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{z}_{2}}+{{m}_{2}}{{z}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right)$
The confusion in writing the above formula is that whether ${{m}_{1}}$ is written with ${{x}_{1}}$ or ${{x}_{2}}$ and similarly with which x value ${{m}_{2}}$ should be written. Similarly, for y and z also this problem occurs. The solution to this confusion is either ${{m}_{1}}$ or ${{m}_{2}}$ the subscript of x should be different from the subscript of m. For instance, in the above formula we have written ${{m}_{1}}$ with ${{x}_{2}}$ so here you can see that subscript of m is 1 and subscript of x is 2 which are different from each other. Likewise you can remember for y and z also.