Question

If ABCD is an isosceles trapezium, then $ \angle C $ is equal to:
(a) $ \angle B $
(b) $ \angle A $
(c) $ \angle D $
(d) Depends on the naming of the trapezium

Answer 1

Hint: Here, we will use the property of an isosceles trapezium to check that which angle is equal to $ \angle C $. There can be two cases depending on the naming of the trapezium. The first case is when $ \angle B $ is adjacent to $ \angle A $ and the second is when $ \angle B $ is on the opposite base to that of $ \angle A $. We will also use the property that the base angles of an isosceles trapezium are equal.

Complete step-by-step answer:
In an isosceles trapezium, two opposite sides are parallel and the two other sides are of equal length. The diagonals are also of equal lengths and the base angles are equal in measure.
The first case is when $ \angle A $ and $ \angle B $ are adjacent to each other.

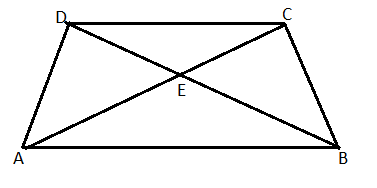
Since, we know that the base angles of a isosceles trapezium are equal. So, $ \angle C $ is equal to $ \angle D $ in this case.
The second case is when $ \angle B $ is on the other base as that of $ \angle A $ .

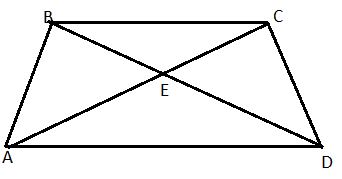
Since, here also as the base angles for an isosceles trapezium are equal, so we can write:
 $ \angle C=\angle B $
Hence, option (d) is the correct answer.

Note: Students should observe here that the naming of the isosceles trapezium is either of the two ways explained above, but it should be kept in mind that the order in which the vertices are given in the problem should not be changed. The naming has to be always done in the order ABCD or it will lead to a mistake.