Question

If ABCD is a square, BD is parallel EF and EG = GF, which one is true?

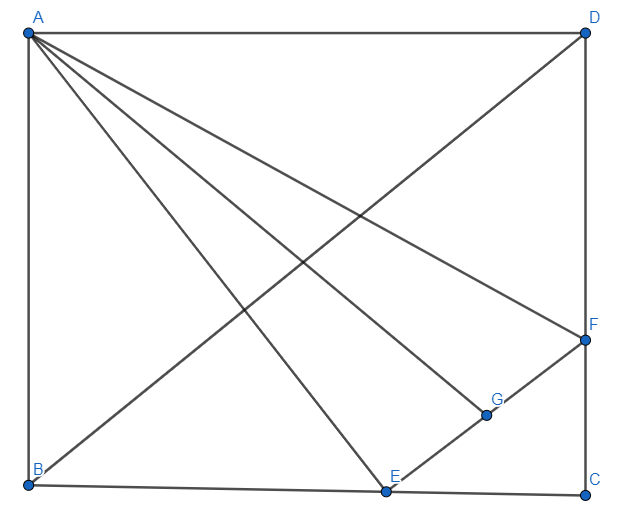
A) BE = FD
B) AG is angular bisector of BAD
C) AG if produced will pass through c
D All of these

Answer 1

Hint:As given that BD is parallel to EF, lines BC and CD will be the traversals for BD and EF. Use the properties that are satisfied by traversal lines between two parallel lines and also given that ABCD is a square which says AB = BC = CD = DA.

Complete step by step answer:
Given that BD is parallel to EF ,
which implies $\dfrac{{CE}}{{EB}} = \dfrac{{CF}}{{FD}} = \dfrac{x}{y}$
Let us take CE = x and EB = y and CF = ax which implies FD = ay
which implies CB = x+y and CD = a(x+y)
As ABCD is a square CB should be equal to CD
which implies a = 1
That says DF = BE = x, CE = CF = y.
So the first option is correct.
Given that EG = GF
We know that ABCD is a square so $\angle $ABE =$\angle $ADF = 90°
And DE = BE and BA = AD
As both triangles, ABE and ADF are right-angled triangles as both the sides of two triangles are equal the remaining side should be equal.
which implies AE = EF.
Now as we know that all the sides of the triangles AEG and AGF are equal all the angles should be equal respectively which implies $\angle $EAG = $\angle $GAF
So AG is angular bisector of BAD
We have known that $\angle $EAG = $\angle $GAF and $\angle $BAE = $\angle $FDA
which implies $\angle $EAG + $\angle $BAE = $\angle $GAF + $\angle $FDA => $\angle $BAE = $\angle $GAD
As $\angle $BAD is right angle $\angle $BAE = $\angle $GAD = 45°
Which says the line BG is angular bisector of the angle A.
In the square we know that the diagonal is itself the angular bisector of any angle, we can say that AG is diagonal.
Therefore AG passes through C when extended.
So all the options are correct.
The correct option is D.

Note:
Do not make assumptions while during geometry related problems. Go through all the axioms and congruencies and similarities. Do not leave the question if you get a single option as correct, because as this sum has more than one answer there can be more than one answer in some questions.