Question

If ABCD is a parallelogram and E, F the centroids of triangles ABD and BCD respectively, then EF equals

(a) AE
(b) BE
(c) CE
(d) DE

Answer 1

Hint: To solve this question, we are going to use the fact that in a triangle ABC,

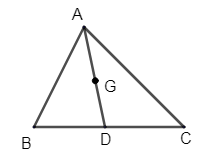
If G is the centroid of the above triangle then, \[\dfrac{AG}{GD}=\dfrac{2}{1}\]. Also, we will use the fact that the triangles ABD and BCD are congruents in the parallelogram.

Complete step-by-step answer:
Before solving the question, we must know what is a parallelogram and what is a centroid in a triangle. A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length. In parallelogram ABCD given in question, AB = CD and AD = BC. A centroid is a point of intersection of all the medians in a triangle.
Now first we will prove that the triangle ABD and triangle BCD are congruent. We know that the sides AB = CD and AD = BC. Also, the side BD is common in both the triangles.
Thus in \[\Delta ABD\] and \[\Delta BCD\], we have
AB = CD
AD = BC
And, BD = BD
Thus the triangles ABD and BCD are congruent. So, here we can say that, AE = CF and OE = OF.
Now, we are going to use a property of a centroid. In \[\Delta ABD\], E is the centroid of the triangles. The centroid E will divide the median in the ratio 2:1. Thus, we can say that,
\[\Rightarrow \dfrac{AE}{EO}=\dfrac{2}{1}\]
\[\Rightarrow AE=2EO\] - (i)
Similarly, in \[\Delta BCD\] F is the centroid of the triangle. The centroid F will divide the median in the ratio 2:1. Thus we can say that,
\[\Rightarrow \dfrac{CF}{FO}=\dfrac{2}{1}\]
\[\Rightarrow CF=2FO\] - (ii)
Now, we know that, AC = AE + ED + FO + CF – (iii)
Now we will put the values of AE and CF from (i) and (ii) into (iii). After doing this, we will get:
\[\begin{align}
  & \Rightarrow AC=2EO+EO+FO+2FO \\
 & \Rightarrow AC=3EO+3FO\left( \because EO=FO \right) \\
 & \Rightarrow AC=3EO+3EO \\
 & \Rightarrow AC=6EO \\
\end{align}\]
\[\Rightarrow EO=\dfrac{AC}{6}\] - (iv)
Now, EF = EO + FO
\[\Rightarrow EF=2EO\]
\[\Rightarrow EF=2\dfrac{AC}{6}\] (From (iv))
\[\Rightarrow EF=\dfrac{AC}{3}\]
Also, AE = 2EO
\[\Rightarrow AE=2\dfrac{AC}{6}\] (From (iv))
\[\Rightarrow AE=\dfrac{AC}{3}\]
Here, we can see that, AE = EF
Hence option (a) is correct.

Note: If the triangles ABD and BCD had been equilateral triangles, then in that case, DE = BE = AE. Thus, in that case, option (a), (b) and (d) had been correct.