Question

If ABCD be a parallelogram and M be the point of intersection of the diagonals. If O is any point then \[OA+OB+OC+OD\] is?
1) \[3OM\]
2) \[4OM\]
3) \[OM\]
4) \[2OM\]
5) \[\dfrac{1}{2}OM\]

Answer 1

Hint: In this problem, we are given ABCD is a parallelogram and M is the point of intersection of the diagonals. If O is any point then we have to find \[OA+OB+OC+OD\]. We can first draw a suitable diagram with the given data, we can then add the given terms by substituting the relevant terms and we know that the diagonals of parallelogram bisect each other, so we can cancel similar terms and get the required value.

Complete step-by-step solution:
We are given ABCD is a parallelogram and M is the point of intersection of the diagonals. If O is any point then we have to find \[OA+OB+OC+OD\].
We can now draw a suitable diagram.

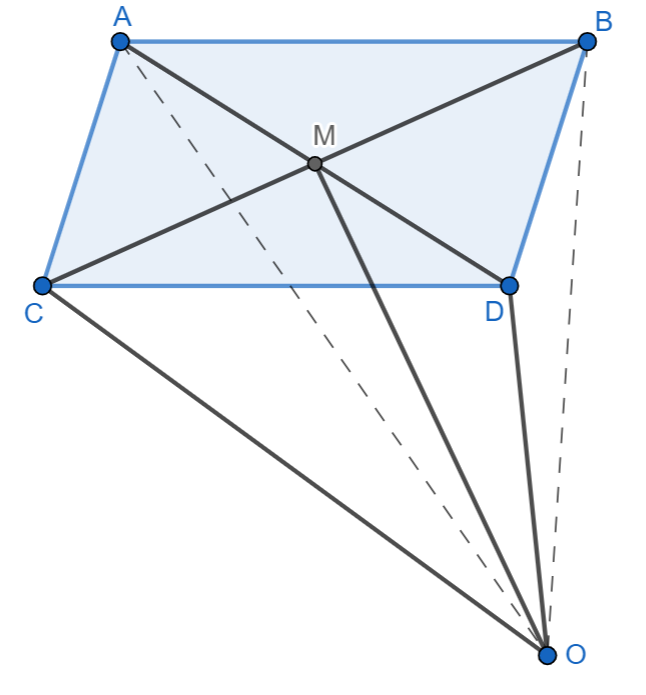
We can now find \[OA+OB+OC+OD\]from the above diagram.
We can see that from the diagram,
\[\begin{align}
  & \Rightarrow OA+AM=OM \\
 & \Rightarrow OB+BM=OM \\
 & \Rightarrow OC+CM=OM \\
 & \Rightarrow OD+DM=OM \\
\end{align}\]
We can now substitute these values, we get
\[\Rightarrow OA+OB+OC+OD=\left( OM-AM \right)+\left( OM-BM \right)+\left( OM-CM \right)+\left( OM-DM \right)\]
We can now add and write the above step as,
\[\Rightarrow OA+OB+OC+OD=4OM-\left( MA+MD+MB+MC \right)\]
We know that the diagonals of the parallelogram bisect each other so we can write\[MA=-MD,MC=-MB\] in the above step,
\[\Rightarrow OA+OB+OC+OD=4OM+\left( MA-MA+MB-MB \right)\]
We can now cancel the similar terms, we get
\[\Rightarrow OA+OB+OC+OD=4OM\]
Therefore, the answer is option 2) \[4OM\].

Note: We should always remember that the diagonals of the parallelogram bisect each other. We should also know to draw a suitable diagram with the given data and add the given terms to get the required answer for it. We can also use the formula method to find the answer for the given question.