Question

If ABC is an isosceles triangle with AB= AC. AD is an altitude of the triangle. Prove that AD is also a median, an angle bisector and a perpendicular bisector of triangle ABC.

Answer 1

Hint: Try proving that the two triangles CAD and BAD are congruent to each other. Note that they have one pair of sides equal and one side common. And since AD is altitude, they are both right-angled triangles. Hence prove that the two triangles are congruent. Since corresponding parts of congruent triangles are equal, prove that AD is a median, a perpendicular bisector and an angle bisector

Complete step-by-step answer:

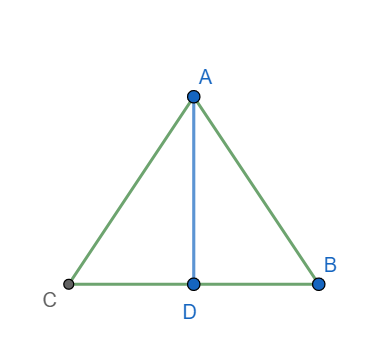
Given: An isosceles triangle ABC with AB = AC. AD is an altitude of the triangle.
To prove: AD is an angle bisector, a median and a perpendicular bisector, the triangle ABC.
Proof:
In triangles ADC and ADB, we have
AD = AD (common side)
AB = AC (Given)
$\angle ADC=\angle ADB$ each 90.
Hence $\Delta ADC\cong \Delta ADB$( By RHS congruence criterion).
Hence we have CD = DB( corresponding parts of the congruent triangles).
Hence AD bisects side CB. Hence AD is a median of the triangle ABC.
Also, $\angle CAD=\angle BAD$( corresponding parts of the congruent triangles).
Hence AD bisects angle A and hence AD is an angle bisector of the triangle ABC.
Also, since AD is perpendicular to BC and AD bisects BC, AD is a perpendicular bisector of the triangle ABC. Hence AD is an altitude, a median, an angle bisector as well as a perpendicular bisector of the triangle ABC. Hence proved.
Note: In these types of questions, it is important to identify which triangles need to be shown congruent. Once the triangles are determined, think about what properties about the two triangles are known and what could be shown so that the triangles are congruent to each other.