
If AB and MN bisect each other at O and AM and BN are perpendicular XY, prove that \[\Delta OAM\] and \[\Delta OBN\] are congruent and hence prove that AM=BN.

Answer
603k+ views
Hint: It is given that AB and MN bisect each other at the point O. So, OA = OB and MO = ON. We know the property that when two lines intersect each other then, the angles opposite to them are equal and known as vertically opposite angles. With the help of this property, we can say that \[\angle AOM=\angle BON\] . In the \[\Delta OAM\] and \[\Delta OBN\] , we have \[\angle AOM=\angle BON\] , OA = OB and MO = ON. Check for congruence of these triangles and solve it further.
Complete step-by-step solution -
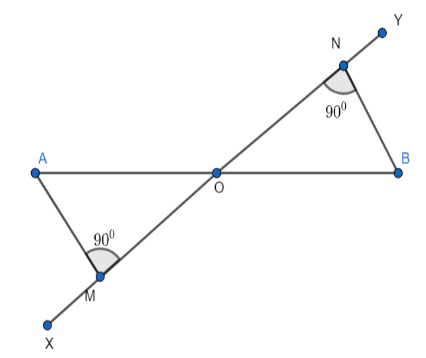
According to the question, we have two lines segments AB and XY which are intersecting at a point O.
We know the property that when two lines intersect each other then, the angles opposite to them are equal and known as vertically opposite angles.
In the figure given, we can say that \[\angle AOM\] and \[\angle BON\]are vertically opposite angles and by using property we can say that both angles are equal.
\[\angle AOM=\angle BON\] ……………………..(1)
It is also given that the line segment AB and the line segment MN bisect each other at the point O.
So, OA = OB ………………………….(2)
MO = ON …………………..(3)
Now, in the triangle \[\Delta OAM\] , we have AM as perpendicular to the line segment XY.
\[\angle AMO={{90}^{0}}\] ………………(4)
We know that the sum of all angles of a triangle is \[{{180}^{0}}\] . So, in triangle \[\Delta OAM\] , we have,
\[\begin{align}
& \angle OAM+\angle AMO+\angle AOM={{180}^{0}} \\
& \Rightarrow \angle OAM+{{90}^{0}}+\angle AOM={{180}^{0}} \\
\end{align}\]
\[\Rightarrow \angle OAM={{90}^{0}}-\angle AOM\] ………………………….(5)
Now, in the triangle \[\Delta OBN\] , we have BN is perpendicular to the line segment XY.
\[\angle BNO={{90}^{0}}\] ………………(6)
We know that the sum of all angles of a triangle is \[{{180}^{0}}\] . So, in triangle \[\Delta OAM\] , we have,
\[\begin{align}
& \angle OBN+\angle BNO+\angle BON={{180}^{0}} \\
& \Rightarrow \angle OBN+{{90}^{0}}+\angle BON={{180}^{0}} \\
\end{align}\]
\[\Rightarrow \angle OBN={{90}^{0}}-\angle BON\] ………………………….(7)
From equation (1), we have \[\angle AOM=\angle BON\] .
Comparing equation (5) and equation (7),
\[\angle OAM={{90}^{0}}-\angle AOM\]
\[\angle OBN={{90}^{0}}-\angle BON\]
\[\angle OBN=\angle OAM\] ……………….(8)
Now, in \[\Delta OAM\] and \[\Delta OBN\] , we have,
OA = OB ………………………….(from equation 2)
\[\angle OAM=\angle OBN\] (from equation 8)
MO = ON …………………..(from equation 3)
Therefore, \[\Delta OAM\cong \Delta OBN\] (side angle side criteria).
The side in front of the \[\angle AOM\] and \[\angle BON\] will be equal.
Hence, AM=BN (congruent part of congruent triangles).
Note: We can also solve this question by another method.
It is given that the line segment AB and the line segment MN bisect each other at the point O.
So, OA = OB ………………(1)
MO = ON …………………..(2)
\[\angle AMO=\angle BNO={{90}^{0}}\] ………………..(3)
Now, in \[\Delta OAM\] and \[\Delta OBN\] , we have,
\[\angle AMO=\angle BNO={{90}^{0}}\]
OA = OB
MO = ON
Therefore, \[\Delta OAM\cong \Delta OBN\] (Right hypotenuse side criteria).
The side in front of the \[\angle AOM\] and \[\angle BON\] will be equal.
Hence, AM=BN (congruent part of congruent triangles).
Complete step-by-step solution -
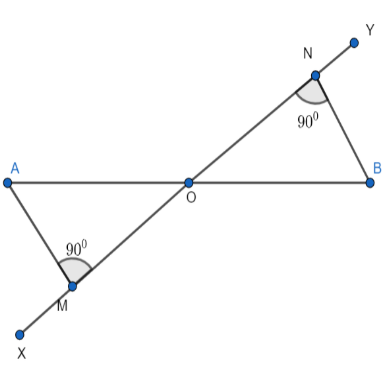
According to the question, we have two lines segments AB and XY which are intersecting at a point O.
We know the property that when two lines intersect each other then, the angles opposite to them are equal and known as vertically opposite angles.

In the figure given, we can say that \[\angle AOM\] and \[\angle BON\]are vertically opposite angles and by using property we can say that both angles are equal.
\[\angle AOM=\angle BON\] ……………………..(1)
It is also given that the line segment AB and the line segment MN bisect each other at the point O.
So, OA = OB ………………………….(2)
MO = ON …………………..(3)
Now, in the triangle \[\Delta OAM\] , we have AM as perpendicular to the line segment XY.
\[\angle AMO={{90}^{0}}\] ………………(4)
We know that the sum of all angles of a triangle is \[{{180}^{0}}\] . So, in triangle \[\Delta OAM\] , we have,
\[\begin{align}
& \angle OAM+\angle AMO+\angle AOM={{180}^{0}} \\
& \Rightarrow \angle OAM+{{90}^{0}}+\angle AOM={{180}^{0}} \\
\end{align}\]
\[\Rightarrow \angle OAM={{90}^{0}}-\angle AOM\] ………………………….(5)
Now, in the triangle \[\Delta OBN\] , we have BN is perpendicular to the line segment XY.
\[\angle BNO={{90}^{0}}\] ………………(6)
We know that the sum of all angles of a triangle is \[{{180}^{0}}\] . So, in triangle \[\Delta OAM\] , we have,
\[\begin{align}
& \angle OBN+\angle BNO+\angle BON={{180}^{0}} \\
& \Rightarrow \angle OBN+{{90}^{0}}+\angle BON={{180}^{0}} \\
\end{align}\]
\[\Rightarrow \angle OBN={{90}^{0}}-\angle BON\] ………………………….(7)
From equation (1), we have \[\angle AOM=\angle BON\] .
Comparing equation (5) and equation (7),
\[\angle OAM={{90}^{0}}-\angle AOM\]
\[\angle OBN={{90}^{0}}-\angle BON\]
\[\angle OBN=\angle OAM\] ……………….(8)
Now, in \[\Delta OAM\] and \[\Delta OBN\] , we have,
OA = OB ………………………….(from equation 2)
\[\angle OAM=\angle OBN\] (from equation 8)
MO = ON …………………..(from equation 3)
Therefore, \[\Delta OAM\cong \Delta OBN\] (side angle side criteria).
The side in front of the \[\angle AOM\] and \[\angle BON\] will be equal.
Hence, AM=BN (congruent part of congruent triangles).
Note: We can also solve this question by another method.
It is given that the line segment AB and the line segment MN bisect each other at the point O.
So, OA = OB ………………(1)
MO = ON …………………..(2)
\[\angle AMO=\angle BNO={{90}^{0}}\] ………………..(3)
Now, in \[\Delta OAM\] and \[\Delta OBN\] , we have,
\[\angle AMO=\angle BNO={{90}^{0}}\]
OA = OB
MO = ON
Therefore, \[\Delta OAM\cong \Delta OBN\] (Right hypotenuse side criteria).
The side in front of the \[\angle AOM\] and \[\angle BON\] will be equal.
Hence, AM=BN (congruent part of congruent triangles).
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




