Question

If $AB = 28$ and $BC = 45$ what is the length in centimetres of $AC$ ?

A) $35$
B) $45$
C) $53$
D) $64$

Answer 1

Hint:
We will first observe that the given triangle is a right-angled triangle as the given angles add up to a right angle. The length of two sides is given so we can use the Pythagorean theorem to find the length of the remaining side. Just add the squares of the given side.

Complete step by step solution:
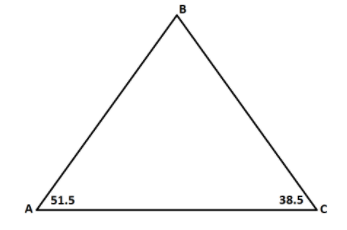
Observe that the given triangle is $\Delta ABC$.
The given lengths are $AB = 28$ and $BC = 45$.
Also, in the diagram it is shown that $\angle A = {51.5^ \circ }$ and $\angle C = {38.5^ \circ }$.
We know that the sum of the measures of all the angles of a triangle is ${180^ \circ }$.
Therefore, we can write:
$\angle A + \angle B + \angle C = {180^ \circ }$
Now out of the three angles values of two angles are already given.
Thus, we write the following:
$51.5 + 38.5 + \angle B = 180$
Solving for the unknown angle we will just take all the remaining terms on the right-hand side.
$\angle B = {90^ \circ }$
Hence, the given angle $\Delta ABC$ is a right-angled triangle.
In the given triangle the hypotenuse is $AC$.
We know that from the Pythagorean theorem we can write that the sum of the squares of the sides that form a right angle is the same as the square of the hypotenuse.
Therefore, we can write the following:
$A{C^2} = A{B^2} + B{C^2}$
Already, we have given the values of the sides $AB$ and $BC$ .
Substituting the given values in the above equation we get the following:
$A{C^2} = {28^2} + {45^2}$
Simplify the squares and add together.
$A{C^2} = 2809$
Taking positive square root, we get,
$AC = 53$

Thus, the correct option is C.

Note:
Note that the given problem is a very basic problem just based on the properties of the right-angled triangle. We just need to observe that the given triangle is a right-angled triangle. In k-12 level one formula can get the work done which is cos rule and sin rule. These rules connect the angle of the triangle with its sides.