Question

If A(1,-2,-1) , B(4,0,-3) ,C(1,2,-1) ,D(2,-4,-5) ,Find the distance between AB and CD.

Answer 1

Hint: Start by preparing the equation of AB and CD in cartesian form. Take points P and Q on AB and CD respectively, find the equation of line PQ . Use the product rule for PQ perpendicular to AB and CD in order to find out coordinates of P and Q. Use the distance formula between P and Q.

Complete step-by-step answer:
Given,
${\text{A}}\left( {{\text{1, - 2, - 1}}} \right){\text{ , B}}\left( {{\text{4,0, - 3}}} \right){\text{ ,C}}\left( {{\text{1,2, - 1}}} \right){\text{ ,D}}\left( {{\text{2, - 4, - 5}}} \right)$
Let us start by finding the equation of line AB and CD
We know equation of line joining two points is given by
$\dfrac{{x - {x_1}}}{{{x_2} - {x_1}}}{\text{ = }}\dfrac{{y - {y_1}}}{{{y_2} - {y_1}}}{\text{ = }}\dfrac{{z - {z_1}}}{{{z_2} - {z_1}}}$
So, Equation of AB ${\text{ = }}\dfrac{{x - 1}}{{4 - 1}}{\text{ = }}\dfrac{{y + 2}}{{0 + 2}}{\text{ = }}\dfrac{{z + 1}}{{ - 3 + 1}}$
$ \Rightarrow {\text{AB = }}\dfrac{{x - 1}}{3}{\text{ = }}\dfrac{{y + 2}}{2}{\text{ = }}\dfrac{{z + 1}}{{ - 2}}$
Let us take a point P on AB
$
  {\text{p = }}\dfrac{{x - 1}}{3}{\text{ = }}\dfrac{{y + 2}}{2}{\text{ = }}\dfrac{{z + 1}}{{ - 2}} \\
   \Rightarrow x = 3p + 1,y = 2p - 2,z = - 2p - 1 \\
  \therefore {\text{P(}}3p + 1,2p - 2, - 2p - 1) \\
$
Similarly, Equation of CD= $\dfrac{{x - 1}}{{2 - 1}}{\text{ = }}\dfrac{{y - 2}}{{ - 4 - 2}}{\text{ = }}\dfrac{{z + 1}}{{ - 5 + 1}}$
$ \Rightarrow {\text{CD = }}\dfrac{{x - 1}}{1}{\text{ = }}\dfrac{{y - 2}}{{ - 6}}{\text{ = }}\dfrac{{z + 1}}{{ - 4}}$
Let us take a point Q on CD
$
  q = {\text{ = }}\dfrac{{x - 1}}{1}{\text{ = }}\dfrac{{y - 2}}{{ - 6}}{\text{ = }}\dfrac{{z + 1}}{{ - 4}} \\
   \Rightarrow x = q + 1,y = - 6q + 2,z = - 4q - 1 \\
  \therefore Q(q + 1, - 6q + 2, - 4q - 1) \\
$
Direction ratios of PQ ${\text{ = (}}3p - q,2p + 6q - 4, - 2p + 4q)$
Now we know that ${\text{PQ}} \bot {\text{AB}}$
So the sum of products of direction ratios will be equal to zero
$
  3(3p - q) + 2(2p + 6q - 4) - 2( - 2p + 4q) = 0 \\
  9p - 3q + 4p + 12q - 8 + 4p - 8q = 0 \\
  17p + q - 8 = 0 \to eqn(1) \\
$

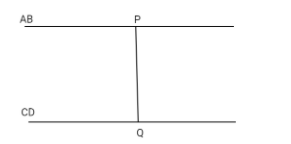
Similarly, ${\text{PQ}} \bot {\text{CD}}$
$
  1(3p - q) - 6(2p + 6q - 4) - 4( - 2p + 4q) = 0 \\
  3p - q - 12p - 36q + 24 + 8p - 16q = 0 \\
   - p - 53q + 24 = 0 \to eqn(2) \\
$
Solving, 17(eqn. 2) + eqn. 1 , we get
$p = \dfrac{4}{9}$
Substituting in eqn. 1 , we get
$q = \dfrac{4}{9}$
$
   \Rightarrow {\text{P(}}\dfrac{4}{9} + 1,\dfrac{{2 \times 4}}{9} - 2,\dfrac{{( - 2) \times 4}}{9} - 1) \\
  \therefore {\text{P(}}\dfrac{{21}}{9},\dfrac{{ - 10}}{9},\dfrac{{ - 17}}{9}) \\
$
Similarly, ${\text{Q(}}\dfrac{{13}}{9},\dfrac{{ - 6}}{9},\dfrac{{ - 25}}{9})$
Here we are not simplifying some of the terms of P and Q , so that the calculation is easy and fast , it won’t affect the result even if we simplify them.
Applying, distance formula between PQ , because it will be equal to the distance between AB and CD
$
  {\text{S = }}\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \\
  {\text{S = }}\sqrt {{{\left( {\dfrac{{21}}{9} - \dfrac{{13}}{9}} \right)}^2} + {{\left( {\dfrac{{ - 10}}{9} + \dfrac{6}{9}} \right)}^2} + {{\left( {\dfrac{{ - 17}}{9} + \dfrac{{25}}{9}} \right)}^2}} \\
  {\text{S = }}\sqrt {{{\left( {\dfrac{8}{9}} \right)}^2} + {{\left( {\dfrac{{ - 4}}{9}} \right)}^2} + {{\left( {\dfrac{8}{9}} \right)}^2}} \\
  {\text{S = }}\sqrt {\dfrac{{64}}{{81}} + \dfrac{{16}}{{81}} + \dfrac{{64}}{{81}}} \\
  {\text{S = }}\sqrt {\dfrac{{144}}{{81}}} \\
  {\text{S = }}\dfrac{4}{3}{\text{units}}{\text{.}} \\
$
Therefore the distance between AB and CD is $\dfrac{4}{3}{\text{units}}{\text{.}}$

Note: All the formulas must be known in both cartesian and vector form in order to solve such similar problems. Dot product and cross product must be practised thoroughly for convenience . Be attentive while substituting values with negative or positive signs, as small mistakes can lead you to the wrong answer.