Question

If a yo-yo is released from your hand with string still wrapped in your hand them the linear acceleration of yo-yo
(A) Much greater than g
(B) Much less them g
(C) Equal to g
(D) None of the above

Answer 1

Hint: In this type of problem first we have to understand the arrangements of yo-yo and tension in the string by weight of yo-yo. Here rotational motion is doing so on applying the formula of torque we will get linear acceleration of yo-yo formula for torque is given as, $\tau = T \times R = I\alpha $
Where $T$=tension, $I$=moment of inertia ,\[\alpha \] =angular momentum and \[\alpha \] is written as, $\alpha = \dfrac{a}{r}$, Where $a$ linear acceleration.

Complete step by step answer:

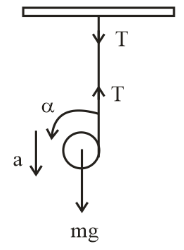
From diagram we can easily calculate the equation of force according to II Newton‘s law
$mg - T = ma$ …..1
Because torque is provided by the tension $\tau = T \times R = I\alpha $
$\alpha = \dfrac{a}{r}$
$\Rightarrow TR = \dfrac{{Ia}}{R}$
$\Rightarrow T = \dfrac{{Ia}}{{{R^2}}}$
On putting the value of T in equation 1
$mg - T = ma$
$\Rightarrow mg - \dfrac{{Ia}}{{{R^2}}} = ma$
$\Rightarrow mg = ma + \dfrac{{Ia}}{{{R^2}}}$
$\Rightarrow g = \dfrac{{ma}}{m} + \dfrac{{Ia}}{{m{R^2}}}$
$\Rightarrow g = a\left( {1 + \dfrac{{Ia}}{{m{R^2}}}} \right)$
$\therefore a = \dfrac{g}{{\left( {1 + \dfrac{I}{{m{R^2}}}} \right)}}$
Because $\dfrac{I}{{m{R^2}}}$ is $ + ve$ then the denominator is greater than 1. So from above expression $a < g$.

So, the motion is downward . Hence option B is the correct answer.

Note: When any particle is attached with spring the weight of particle is balanced by tension of spring but if an extra acceleration is given to particle then tension is balanced by weight and external force both depending on acceleration is given in what direction.