Question

If a tangent to the parabola $ {{y}^{2}}=4ax $ meets the $ x- $ axis at $ T $ and the tangent at the vertex $ A $ in $ P $ and the rectangle $ TAPQ $ is completed. Then the locus of $ Q $ is;
A. $ {{y}^{2}}+4ax=0 $ \[\]
B. $ {{y}^{2}}+2ax=0 $ \[\]
C. $ {{y}^{2}}=2ax $ \[\]
D. $ {{y}^{2}}+ax=0 $ \[\]

Answer 1

Hint: We take the point of contact of tangent in parametric form as $ \left( a{{t}^{2}},2at \right) $ which gives us equation of the tangent $ ty=x+a{{t}^{2}} $ . We denote the coordinate of Q as $ Q\left( h,k \right) $ for instance. We find the coordinates of $ A,P,T $ . We use the fact that diagonals in a rectangle bisect each other and find the equate the coordinates of midpoints of diagonal TP and AQ. We find $ h,k $ in terms of $ t $ . We eliminate $ t $ and replace $ \left( h,k \right) $ by $ \left( x,y \right) $ to get the focus. \[\]

Complete step by step answer:
We are given in the question the equation of rightward parabola $ {{y}^{2}}=4ax $ meets the $ x- $ axis at $ T $ and the tangent vertex $ A $ in $ P $ . We know that any point on the parabola $ {{y}^{2}}=4ax $ with a parameter $ t $ is given by $ \left( a{{t}^{2}},2at \right) $ and the equation of the tangent at the point $ \left( a{{t}^{2}},2at \right) $ is given by

\[ty=x+a{{t}^{2}}\]
Let the $ V\left( a{{t}^{2}},2at \right) $ be the variable point where our given tangent with equation $ ty=x+a{{t}^{2}} $ is drawn which meets the $ x- $ axis at $ T $ and the tangent vertex $ A $ in $ P $ . Let us assume the fourth vertex $ Q $ of the rectangle at one instance has coordinate $ Q\left( h,k \right) $ . We have the rough figure as; \[\]

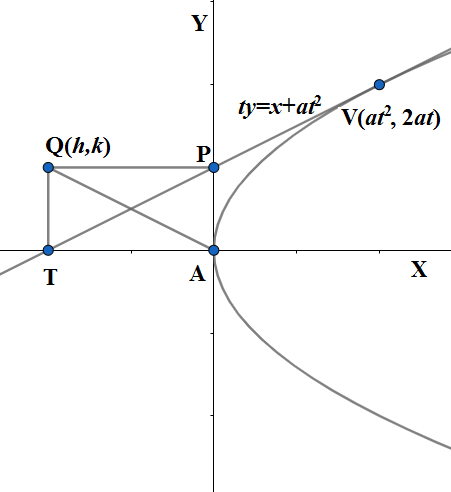
Let us find the other 3 coordinates of vertices of the rectangle TAPQ. Since all parabolas of the type $ {{y}^{2}}=4ax $ have the coordinate of their vertex at the origin the coordinate of $ A $ is $ A\left( 0,0 \right) $ and tangent at the vertex is $ y- $ axis. Since all the points on $ x- $ axis like $ T $ has their $ y- $ coordinate zero and also $ T $ lies on the tangent $ ty=x+a{{t}^{2}} $ we have;
\[\begin{align}
  & t\left( 0 \right)=x+a{{t}^{2}} \\
 & \Rightarrow x=-a{{t}^{2}} \\
\end{align}\]
So the coordinate of $ T $ is $ T\left( -a{{t}^{2}},0 \right) $ . Since all the points on $ y- $ axis like $ P $ has their $ y- $ coordinate zero and also $ P $ lies on the tangent $ ty=x+a{{t}^{2}} $ we have;
\[\begin{align}
  & ty=0+a{{t}^{2}} \\
 & \Rightarrow y=at \\
\end{align}\]
So the coordinate of $ P $ is $ P\left( 0,at \right) $ . Let us denote the point of intersection of diagonals TP and AQ as M.

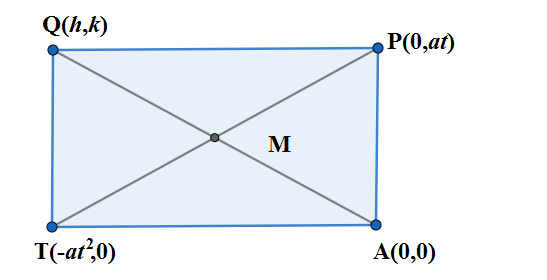
Since the midpoints of the diagonals QA and TP will be same and that is M irrespective of motion of the point Q, we use the midpoint formula and have the coordinate of M as ;
\[\begin{align}
  & \text{midpoint of TP}=\text{midpoint of AQ} \\
 & \Rightarrow \left( \dfrac{-a{{t}^{2}}+0}{2},\dfrac{0+at}{2} \right)=\left( \dfrac{0+h}{2},\dfrac{0+k}{2} \right) \\
 & \Rightarrow \left( \dfrac{-a{{t}^{2}}}{2},\dfrac{at}{2} \right)=\left( \dfrac{h}{2},\dfrac{k}{2} \right) \\
 & \Rightarrow \dfrac{h}{2}=\dfrac{-a{{t}^{2}}}{2},\dfrac{k}{2}=\dfrac{at}{2} \\
 & \Rightarrow h=-a{{t}^{2}},k=at \\
\end{align}\]
Let us eliminate $ t $ from the above equations.
\[\begin{align}
  & \because k=at\Rightarrow t=\dfrac{k}{a} \\
 & h=-a{{t}^{2}} \\
 & \Rightarrow h=-a{{\left( \dfrac{k}{a} \right)}^{2}} \\
 & \Rightarrow h=-a\dfrac{{{k}^{2}}}{{{a}^{2}}} \\
 & \Rightarrow {{k}^{2}}+ah=0 \\
\end{align}\]
Let us replace $ \left( h,k \right) $ by $ \left( x,y \right) $ for all instances during the motion of Q. We have the locus of $ Q $ as;
\[{{y}^{2}}+ax=0\]
So the correct option is D. \[\]
Note:
We know that if $ \left( {{x}_{1}},{{y}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}} \right) $ be two end points of a lines segment the coordinates of the midpoint is given by $ \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right) $ . We can alternatively find $ h,k $ in terms of $ t $ by observing that the $ x- $ coordinates of all points of line parallel $ y- $ axis like T and Q and the $ y- $ coordinates of all points of line parallel $ y- $ axis like Q and P will be same. We can also use the equation of tangent to the parabola $ {{y}^{2}}=4ax $ in slope-point from $ y=mx+\dfrac{a}{m} $ to solve the problem quickly.