Question

If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
(A) 2r
(B) r
(C) 4r
(D) 3r

Answer 1

Hint:Solid sphere is melted and cast into a solid cone so the volume of solid sphere and volume of solid cone is the same. First of all, we have to compare both the volume of solid sphere to volume of solid cone. Then find the value of the radius of the base of the solid cone.

Formula used:
\[V = \dfrac{4}{3}\pi {r^3}\]; Where, $r$ is the radius of the solid sphere and we don’t substitute the value of $\pi$.
The formula for calculating the volume of solid cone is:
\[V = \dfrac{1}{3}\pi {R^2}h\]; Where $R$ is the radius of base of the solid cone and $h$ is the height of the solid cone.

Complete step-by-step answer:
Solid sphere is melted and cast into a solid cone so the volume of solid sphere and volume of solid cone is the same.

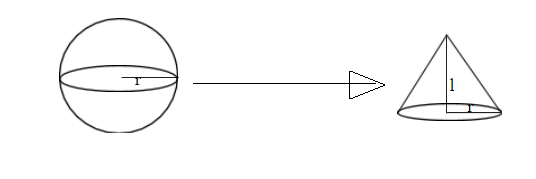
\[{V_{sphere}}={V_{cone}}\] ....(Equation 1)
The volume of the solid sphere of radius r is given by:
\[{V_{sphere}} = \dfrac{4}{3}\pi {r^3}\]
The height of solid cone is r and assume that the radius of base of the cone is R.so the volume of the solid cone is given by
\[{V_{cone}} = \dfrac{1}{3}\pi {R^2}h\]
$\Rightarrow$\[ = \dfrac{1}{3}\pi {R^2}r\]
$\Rightarrow$\[\dfrac{4}{3}\pi {r^3} = \dfrac{1}{3}\pi {R^2}r\]
Cancel out the same terms from both sides of the equation.
$\Rightarrow$\[R = 2r\]
The radius of the base of the solid cone is double of the radius of the solid sphere.

$\therefore$ The radius of the base of the solid cone is double of the radius of the solid sphere. So, Option A is correct.

Note:
In question the statement that a solid sphere of radius $r$ is melted and cast into the shape of a solid cone of height $r$ is to solve the whole problem. Some students do not properly read the statement of the example so they make a mistake.