Question

If a regular hexagon is inscribed in a circle of radius $r,$ what its perimeter.
(A) $3r$
(B) $6r$
(C) $9r$
(D) $12r$

Answer 1

Hint: Given that a regular hexagon is inscribed in a circle of radius $r$. Try to prove that a hexagonal is made of size equilateral triangles by joining the opposite sides of the hexagon; after that you will observe that each side of the equilateral triangle is ’$r$’ which is equal to the radius of the circle. Now, you can easily find the perimeter of the hexagon.

Complete step-by-step solution:
Given in the question that a regular hexagon is inscribed in a circle of radius ‘$r$’.
So, it is inside the circle
By joining the opposite comer of the hexagon it forms size central angles at centre $O.$ as shown in figure
Each angles forms at centre of can be calculated by dividing $360$ degrees with $6$
Since, a circle has a total of $360$ degrees all the way around the centre.
Therefore Each angle forming $=\dfrac{360}{6}=60{}^\circ $ at centre

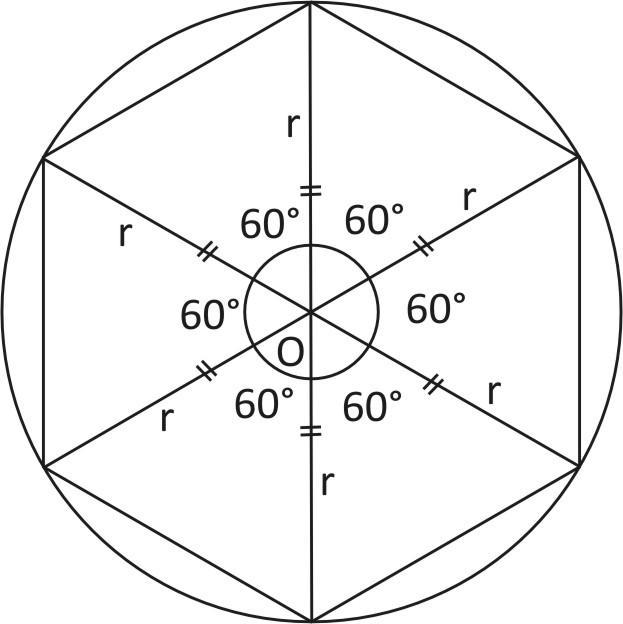
Also, you see the six triangles are formed to consider one triangle among the six triangles. The two ideas of triangle are the radius of the circle since joining form the centre to the circumference of the circle and thus are equal.
Therefore, the base angles of the triangle are also equal as by equality property.
Now, the central angle is $60{}^\circ $
We know that sum of all angles of triangle is $180{}^\circ $

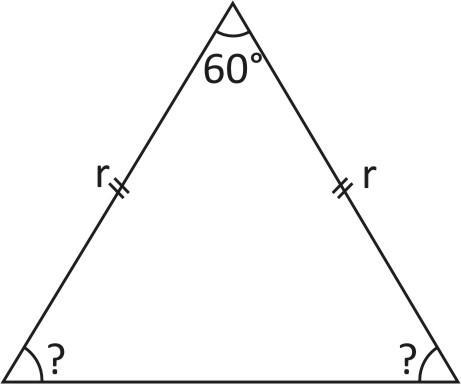
Therefore Base angles $=\dfrac{\text{Sum of Remaining angle}}{2}$
Therefore Base angles $=\dfrac{120{}^\circ }{2}=60{}^\circ $
Therefore, all angles of the triangle are $60{}^\circ ,$ the triangle is said to be an equilateral triangle.
Similarly, we can say that all 6 triangles which are formed are equilateral triangles since the above explanation applies for all triangles.
This gives all sides of the triangle equal.
Therefore, we can say that all sides of each triangle is equal to ‘$r$’.
Now, the perimeter of the Hexagon can be calculated by sum of all sides of the hexagon.
$=r+r+r+r+r$
$=6r$
Hence, perimeter of regular hexagon is $6r$

Therefore, option $B$ is correct.

Note: A regular hexagon is defined as a hexagon that is both equilateral and equiangular.
An equilateral triangle is a triangle in which all three sides have the same length. Also an equilateral triangle is equiangular each of $60{}^\circ $.
Always remember that in a circle the sum of the central angle is equal to $360$ degrees and, also the sum of all angles in a triangle is $180{}^\circ $ degree.