Question

If a quadrilateral ABCD such that $\overrightarrow {AB} = b$ , $\overrightarrow {AD} = d$ and $\overrightarrow {AC} = pb + qd$ $p + q \geqslant 1$ , then show that the area of the quadrilateral is $\dfrac{1}{2}(p + q)\left| {b \times d} \right|$ .

Answer 1

Hint: First find the area of triangle ABC by using $\dfrac{1}{2}\left| {\overrightarrow {AB} \times \overrightarrow {BC} } \right|$ where $\overrightarrow {AB} = b$ and \[\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \]
similarly find the area of triangle ADC by using $\dfrac{1}{2}\left| {\overrightarrow {AD} \times \overrightarrow {DC} } \right|$ where $\overrightarrow {AD} = d$ and \[\overrightarrow {DC} = \overrightarrow {AC} - \overrightarrow {AB} \] now add both area we get the area of quadrilateral .

Complete step-by-step answer:
As it is given that the quadrilateral ABCD such that $\overrightarrow {AB} = b$ , $\overrightarrow {AD} = d$ and $\overrightarrow {AC} = pb + qd$ $p + q \geqslant 1$ , we have to prove that the area of the quadrilateral is $\dfrac{1}{2}(p + q)\left| {b \times d} \right|$
So for this first draw the figure by the given information ,

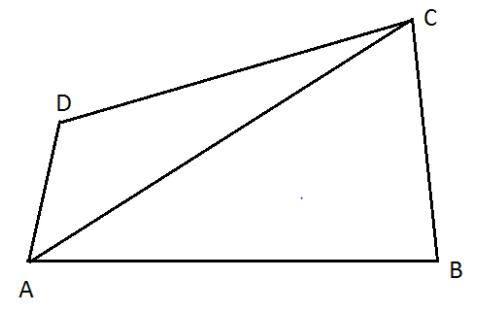
So in triangle ABC we know from the triangle law ,
$\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} $
And \[\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \]
In the question it is given that the $\overrightarrow {AB} = b$ and $\overrightarrow {AC} = pb + qd$
on putting these values we get
\[\overrightarrow {BC} = pb + qd - b\]
or \[\overrightarrow {BC} = \left( {p - 1} \right)b + qd\]
As we know the area of triangle can be written as $\dfrac{1}{2}\left| {\overrightarrow {AB} \times \overrightarrow {BC} } \right|$
Put the values of it ,
\[\dfrac{1}{2}\left| {b \times \left( {\left( {p - 1} \right)b + qd} \right)} \right|\]
So we know that , the cross product to itself is zero mean that $\overrightarrow b \times \overrightarrow b = 0$ from this ,
Area of triangle ABC \[\dfrac{q}{2}\left| {b \times d} \right|\] .......(i)
Now for the triangle ADC we know from the triangle law ,
$\overrightarrow {AD} + \overrightarrow {DC} = \overrightarrow {AC} $
And \[\overrightarrow {DC} = \overrightarrow {AC} - \overrightarrow {AB} \]
In the question it is given that the $\overrightarrow {AD} = d$ and $\overrightarrow {AC} = pb + qd$
on putting these values we get
\[\overrightarrow {DC} = pb + qd - d\]
or \[\overrightarrow {DC} = pb + (q - 1)d\]
As we know the area of triangle can be written as $\dfrac{1}{2}\left| {\overrightarrow {AD} \times \overrightarrow {DC} } \right|$
Put the values of it ,
\[\dfrac{1}{2}\left| {d \times \left( {pb + (q - 1)d} \right)} \right|\]
So we know that , the cross product to itself is zero mean that $\overrightarrow d \times \overrightarrow d = 0$ from this ,
Area of triangle ADC \[\dfrac{p}{2}\left| {d \times b} \right|\] .......(ii)
Now for the area of quadrilateral ABCD = Area of ABC + Area of ADC
From (i) and the (ii) put the values of area ,
 area of quadrilateral ABCD = \[\dfrac{q}{2}\left| {b \times d} \right|\] +\[\dfrac{p}{2}\left| {d \times b} \right|\]
As we know that $\left| {b \times d} \right| = \left| {d \times b} \right|$ so from using this
Area of quadrilateral ABCD = $\dfrac{1}{2}(p + q)\left| {b \times d} \right|$
Hence proved

Note: Cross product always gives the vector which is perpendicular to the both vectors and its direction would be determined by Right hand rule .
The dot product tells you what amount of one vector goes in the direction of another .
Dot product of the perpendicular vector is always zero .