Question

If a positively charged pendulum is oscillating in a uniform electric field as shown in figure. Its time period as compared to that when it was uncharged:

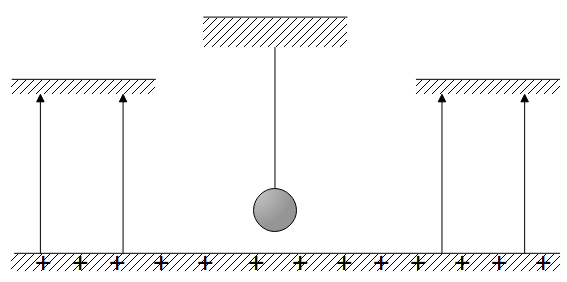
(A) Will increase
(B) will decrease
(C) will not change
(D) will first increase then decrease

Answer 1

Hint: The given pendulum is present in the region where the electric field is opposing the gravitational field. The resultant of the two forces will give the net gravitational force that the bob experiences in the downwards direction and that g’ will determine the time period.
Formula Used:
The time period of a simple pendulum performing small oscillations is given as:
$T = 2\pi \sqrt {{g \over l}} $
where l is the length of the pendulum and g is the acceleration due to gravity.

Complete answer:
Consider the following free body diagram of the given pendulum:

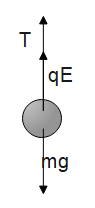
Total forces acting on the given pendulum are: (1) Tension of the string, (2) gravity, (3) electric force due to the field. While, if we consider the case of a general simple pendulum we have two forces only- tension and gravity (balancing each other).
Thus, for the case of a given pendulum we can say that the electric field is exerting a force on the given pendulum such that it pushes the pendulum upwards i.e., along the arrows. The resultant gravitational force that creates a g’ downwards now can be found as:
$\eqalign{
  & mg' = mg - qE \cr
  & \Rightarrow g' = g - {{qE} \over m} \cr} $
Therefore a simple conclusion follows from here that as the g’ obtained will be obviously less than the g, we can say that the time period which is directly proportional to the square root of g will decrease as g becomes g’ for the given pendulum and g’ is less than g.

Therefore the correct option is (B).

Note:
The electric field acts from positive end of the plates to negative end. As the positive end is placed below, it will do the job of repelling our positively charged bob. When we place a positive charge in the electric field, it moves along it and negative charge goes in the opposite direction of the arrows.